Question

9．在平面直角坐标系xOy中，设A，B分别为曲线y=$\sqrt{1{-x}^{2}}$与x轴的两个交点，C、D分别为曲线上的两个动点，则$\overrightarrow{AC}•\overrightarrow{BD}$的取值范围是[-4，$\frac{1}{2}$]．

Answer 1

分析 由向量的几何意义，以及直线和圆的位置关系即可求出．

解答 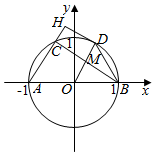解：曲线y=$\sqrt{1{-x}^{2}}$为半圆，如图所示：A（-1，0），B（1，0），
当$\overrightarrow{AC}$，$\overrightarrow{BD}$方向相反时，且长度均为2时，$\overrightarrow{AC}•\overrightarrow{BD}$=-4，
设D在$\overrightarrow{AC}$上的投影点为H，OD与BC的交于点M，OM=x，
则当DH为圆0的切线时，$\overrightarrow{AC}•\overrightarrow{BD}$=|$\overrightarrow{AC}$|•|$\overrightarrow{CH}$|=2x（1-x）≤$\frac{1}{2}$，（当且仅当x=$\frac{1}{2}$时等号成立）
所以则$\overrightarrow{AC}•\overrightarrow{BD}$的取值范围是[-4，$\frac{1}{2}$]

点评 本题考查了向量的几何意义，关键是掌握点位置关系，以及直线和圆的位置关系，属于中档题．