
分析 (Ⅰ)要使函数f(x)=$\sqrt{|x+1|+|x-2|+a}$有意义,则|x+1|+|x-2|-5≥0.然后对x分类讨论去绝对值求解;
(Ⅱ)函数f(x)的定义域为R,则|x+1|+|x-2|+a≥0恒成立.即|x+1|+|x-2|≥-a恒成立.构造函数h(x)=|x+1|+|x-2|,写出分段函数解析式,求出最小值得答案.
解答 解:(Ⅰ)当a=-5时,要使函数f(x)=$\sqrt{|x+1|+|x-2|+a}$有意义,
则|x+1|+|x-2|-5≥0.
①当x≤-1时,原不等式可化为-x-1-x+2-5≥0,即x≤-2;
②当-1<x<2时,原不等式可化为x+1-x+2≥5,即3≥5,显然不成立;
③当x≥2时,原不等式可化为x+1+x-2≥5,即x≥3.
综上所求函数的定义域为(-∞,-2]∪[3,+∞);
(Ⅱ)函数f(x)的定义域为R,则|x+1|+|x-2|+a≥0恒成立.
即|x+1|+|x-2|≥-a恒成立.
构造函数h(x)=|x+1|+|x-2|=$\left\{\begin{array}{l}{1-2x,x≤-1}\\{3,-1<x<2}\\{2x-1,x≥2}\end{array}\right.$,求得函数的最小值为3.
∴a≥-3.
点评 本题考查函数的定义域及其求法,考查分类讨论的数学思想方法及数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该四棱锥的所有棱中,最长的棱的长度为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该四棱锥的所有棱中,最长的棱的长度为( )| A. | $\sqrt{41}$ | B. | $\sqrt{34}$ | C. | 5 | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (4,+∞) | C. | (2,4] | D. | [2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 回归分析和独立性检验没有什么区别 | |
| B. | 回归分析是对两个变量准确关系的分析,而独立性检验是分析两个变量之间的不确定关系 | |
| C. | 回归分析研究两个变量之间的相关关系,独立性检验是对两个变量是否具有某种关系的一种检验 | |
| D. | 独立性检验可以100%确定两个变量之间是否具有某种关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
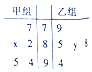 下列茎叶图记录了甲、乙两组各五名学生在一次数学测试中的成绩(单位:分),已知甲组数据的平均数为86,乙组数据的中位数为86,则x,y的值分别为( )
下列茎叶图记录了甲、乙两组各五名学生在一次数学测试中的成绩(单位:分),已知甲组数据的平均数为86,乙组数据的中位数为86,则x,y的值分别为( )| A. | 2,7 | B. | 2,6 | C. | 3,7 | D. | 3,6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com