
| A. | 如果直线l与平面α内无数条直线成异面直线,则l∥α | |
| B. | 如果直线l与平面α内无数条直线平行,则l∥α | |
| C. | 如果直线l与平面α内无数条直线成异面直线,则l?α | |
| D. | 如果一条直线与一个平面平行,则该直线平行于这个平面内的所有直线 | |
| E. | 如果一条直线上有无数个点不在平面内,则这条直线与这个平面平行 |
分析 在A中,l与α平行或相交;在B中,l与α平行或l?α;在C中,l与α平行或相交,即l?α;在D中,该直线与这个平面内的所有直线平行或异面;在E中,这条直线与这个平面平行或相交.
解答 解:在A中,如果直线l与平面α内无数条直线成异面直线,则l与α平行或相交,故A错误;
在B中,如果直线l与平面α内无数条直线平行,则l与α平行或l?α,故B错误;
在C中,如果直线l与平面α内无数条直线成异面直线,则l与α平行或相交,即l?α,故C正确;
在D中,如果一条直线与一个平面平行,则该直线与这个平面内的所有直线平行或异面,故D错误;
在E中,如果一条直线上有无数个点不在平面内,则这条直线与这个平面平行或相交,故E错误.
故选:C.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≤n | B. | m<n | C. | m≥n | D. | m>n |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
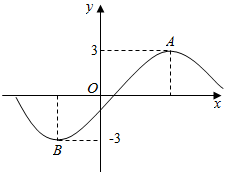 已知函数f(x)=3sin(ωx+φ)(ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,A、B两点之间的距离为10,且f(2)=0,若将函数f(x)的图象向右平移t(t>0)个单位长度后所得函数图象关于y轴对称,则t的最小值为6.
已知函数f(x)=3sin(ωx+φ)(ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,A、B两点之间的距离为10,且f(2)=0,若将函数f(x)的图象向右平移t(t>0)个单位长度后所得函数图象关于y轴对称,则t的最小值为6.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com