
分析 (Ⅰ)利用等差数列以及等比数列的关系,求出数列的首项与公差,然后求数列{an}的通项公式;
(Ⅱ)化简通项公式,利用错位相减法求和求解即可.
解答 (Ⅰ)解:根据题意,等差数列{an}中,设公差为d,a4=2a2,且a1,4,a4成等比数列,a1>0,
即$\left\{\begin{array}{l}{a_1}+3d=2({a_1}+d)\\{a_1}•({a_1}+3d)=16\end{array}\right.$解得a1=2,d=2,
所以数列{an}的通项公式为an=a1+(n-1)d=2+2(n-1)=2n.
(Ⅱ)证明:由(Ⅰ)知a1=d=2,则${S_n}=2n+\frac{n(n-1)}{2}×2={n^2}+n$,
∴${b_n}=\frac{S_n}{{n•{2^n}}}=\frac{n+1}{2^n}$.
∴${T_n}=\frac{2}{2^1}+\frac{3}{2^2}+\frac{4}{2^3}+…+\frac{n+1}{2^n}$,(*)$\frac{1}{2}{T_n}=\frac{2}{2^2}+\frac{3}{2^3}+…+\frac{n}{2^n}+\frac{n+1}{{{2^{n+1}}}}$,(**)
∴$\frac{1}{2}{T_n}=\frac{2}{2^1}+\frac{1}{2^2}+\frac{1}{2^3}+…+\frac{1}{2^n}-\frac{n+1}{{{2^{n+1}}}}$,
∴${T_n}=2+\frac{1}{2^1}+\frac{1}{2^2}+…+\frac{1}{{{2^{n-1}}}}-\frac{n+1}{2^n}=2+\frac{{\frac{1}{2}(1-\frac{1}{{{2^{n-1}}}})}}{{1-\frac{1}{2}}}-\frac{n+1}{2^n}=3-\frac{1}{{{2^{n-1}}}}-\frac{n+1}{2^n}<3$.
∴Tn<3.
点评 本题考查等差数列的应用,数列求和的方法,考查计算能力.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{5π}{6},\frac{π}{6}}]$ | B. | $[{-\frac{π}{3},\frac{π}{6}}]$ | C. | $[{-\frac{5π}{12},\frac{π}{12}}]$ | D. | $[{\frac{π}{12},\frac{7π}{12}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,n∥α,则m∥n | B. | 若m⊥α,n⊥α,则m∥n | C. | 若m⊥n,n?α,则m⊥α | D. | 若m∥n,m∥α,则n∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
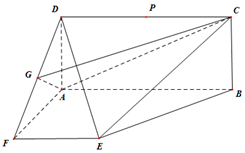 已知矩形ABCD与直角梯形ABEF,∠DAF=∠FAB=90°,点G为DF的中点,AF=EF=$\frac{1}{2}AB=\sqrt{3}$,P在线段CD上运动.
已知矩形ABCD与直角梯形ABEF,∠DAF=∠FAB=90°,点G为DF的中点,AF=EF=$\frac{1}{2}AB=\sqrt{3}$,P在线段CD上运动.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\frac{{\sqrt{3}}}{3}$ | B. | ±1 | C. | $±\sqrt{3}$ | D. | ±2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | λ2+μ2=1 | B. | $\frac{1}{λ}$+$\frac{1}{μ}$=1 | C. | λ•μ=1 | D. | λ+μ=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{3π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com