
【题目】抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 是抛物线上的两个动点,线段
是抛物线上的两个动点,线段![]() 的中点为
的中点为![]() ,过
,过![]() 作抛物线准线的垂线,垂足为
作抛物线准线的垂线,垂足为![]() ,若
,若![]() ,则
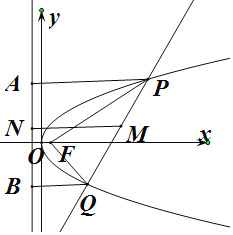
,则![]() 的最大值为______.
的最大值为______.
【答案】![]()
【解析】分析:设|PF|=2a,|QF|=2b,.由抛物线定义得|PQ|=a+b,由余弦定理可得(a+b)2=4a2+4b2﹣8abcosθ,进而根据基本不等式,求得的θ取值范围,从而得到本题答案.
详解:设|PF|=2a,|QF|=2b,
由抛物线定义,得|PF|=|PA|,|QF|=|QB|,
在梯形ABPQ中,2|MN|=|PA|+|QF|=2a+2b,
∵|MN|=|PQ|,
∴|PQ|=a+b,
由余弦定理得,设∠PFQ=θ,
(a+b)2=4a2+4b2﹣8abcosθ,
∴a2+b2+2ab=4a2+4b2﹣8abcosθ,
∴cosθ=![]() ,当且仅当a=b时取等号,
,当且仅当a=b时取等号,
∴θ≤![]() ,
,
故答案为:![]()


科目:高中数学 来源: 题型:
【题目】某校为“中学数学联赛”选拔人才,分初赛和复赛两个阶段进行,规定:分数不小于本次考试成绩中位数的具有复赛资格,某校有900名学生参加了初赛,所有学生的成绩均在区间![]() 内,其频率分布直方图如图.
内,其频率分布直方图如图.

(1)求获得复赛资格应划定的最低分数线;
(2)从初赛得分在区间![]() 的参赛者中,利用分层抽样的方法随机抽取7人参加学校座谈交流,那么从得分在区间
的参赛者中,利用分层抽样的方法随机抽取7人参加学校座谈交流,那么从得分在区间![]() 与
与![]() 各抽取多少人?
各抽取多少人?
(3)从(2)抽取的7人中,选出4人参加全市座谈交流,设![]() 表示得分在
表示得分在![]() 中参加全市座谈交流的人数,学校打算给这4人一定的物质奖励,若该生分数在
中参加全市座谈交流的人数,学校打算给这4人一定的物质奖励,若该生分数在![]() 给予500元奖励,若该生分数在
给予500元奖励,若该生分数在![]() 给予800元奖励,用Y表示学校发的奖金数额,求Y的分布列和数学期望。
给予800元奖励,用Y表示学校发的奖金数额,求Y的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为抛物线
为抛物线![]() 上异于原点的任意一点,过点
上异于原点的任意一点,过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于另一点
于另一点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,且有
,且有![]() .当点
.当点![]() 的横坐标为3时,
的横坐标为3时,![]() 为正三角形.
为正三角形.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() ,且
,且![]() 和抛物线
和抛物线![]() 有且只有一个公共点
有且只有一个公共点![]() ,试问直线
,试问直线![]() 是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有关于x的一元二次方程![]() .
.
![]() 若a是从0,1,2三个数中任取的一个数,b是从0,1,2,3四个数中任取的一个数,求上述方程有实根的概率;
若a是从0,1,2三个数中任取的一个数,b是从0,1,2,3四个数中任取的一个数,求上述方程有实根的概率;
![]() 若a是从区间
若a是从区间![]() 任取的一个数,b是从区间
任取的一个数,b是从区间![]() 任取的一个数,求上述方程有实数的概率.
任取的一个数,求上述方程有实数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用7局4胜制(即先胜4局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
(1)求乙以4比1获胜的概率;
(2)求甲获胜且比赛局数多于5局的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度后,再将所得的图象向下平移一个单位长度得到函数
个单位长度后,再将所得的图象向下平移一个单位长度得到函数![]() 的图象,且
的图象,且![]() 的图象与直线
的图象与直线![]() 相邻两个交点的距离为
相邻两个交点的距离为![]() ,若
,若![]() 对任意
对任意![]() 恒成立,则
恒成立,则![]() 的取值范围是 ( )
的取值范围是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为减少空气污染,某市鼓励居民用电(减少粉尘),并采用分段计费的方法计算电费.当每个家庭月用电量不超过100千瓦时时,按每千瓦时0.57元计算;当月用电量超过100千瓦时时,其中的100千瓦时仍按原标准收费,超过的部分按每千瓦时0.5元计算.
(1)设月用电x千瓦时时,应交电费y元,写出y关于x的函数关系式;
(2)若某家庭一月份用电120千瓦时,则应交电费多少元?
(3)若某家庭第一季度缴纳电费的情况如下表:
月份 | 1月 | 2月 | 3月 | 合计 |
交费金额(元) | 76 | 63 | 45.6 | 184.6 |
则这个家庭第一季度共用电多少千瓦时?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为提升教师专业功底,引领青年教师成长,某市教育局举行了全市“园丁杯”课堂教学比赛.在这次比赛中,通过采用录像课评比的片区预赛,有![]() 共10位选手脱颖而出进入全市决赛.决赛采用现场上课形式,从学科评委库中采用随机抽样选代号
共10位选手脱颖而出进入全市决赛.决赛采用现场上课形式,从学科评委库中采用随机抽样选代号![]() 的7名评委,规则是:选手上完课,评委当场评分,并从7位评委评分中去掉一个最高分,去掉一个最低分,根据剩余5位评委的评分,算出平均分作为该选手的最终得分.记评委
的7名评委,规则是:选手上完课,评委当场评分,并从7位评委评分中去掉一个最高分,去掉一个最低分,根据剩余5位评委的评分,算出平均分作为该选手的最终得分.记评委![]() 对某选手评分排名与该选手最终排名的差的绝对值为“评委
对某选手评分排名与该选手最终排名的差的绝对值为“评委![]() 对这位选手的分数排名偏差” (
对这位选手的分数排名偏差” (![]() ).排名规则:由高到低依次排名,如果选手分数一样,认定名次并列(如:选手
).排名规则:由高到低依次排名,如果选手分数一样,认定名次并列(如:选手![]() 分数一致排在第二,则认为他们同属第二名,没有第三名,接下来分数为第四名).七位评委评分情况如图所示:
分数一致排在第二,则认为他们同属第二名,没有第三名,接下来分数为第四名).七位评委评分情况如图所示:
(Ⅰ)根据最终评分表,填充如下表格,并完成评委4和评委5对十位选手的评分的茎叶图;

(Ⅱ)试根据评委对各选手的排名偏差的平方和,判断评委4和评委5在这次活动中谁评判更准确.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com