
| A. | [2,+∞) | B. | $[0,\frac{1}{3}]$ | C. | $[\frac{1}{3},3]$ | D. | (-∞,3) |
分析 画出满足不等式组表示的平面区域,根据平面区域里的点,利用目标函数z=ax+y的最大值为3a,构造关于a的不等式组,解不等式组求出a的取值范围.
解答 解:画出不等式组$\left\{\begin{array}{l}x+y-1≥0\\ x-2y+2≥0\\ 2x-y-2≤0\end{array}\right.$表示的平面区域如图所示,
由图可知,求出三条边界直线的交点分别为: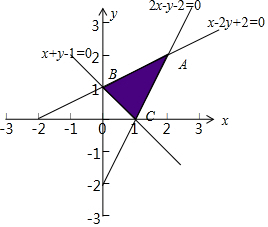
B(0,1),A(2,2),C(1,0).
由目标函数z=ax+y的最大值不大于3a,
将这三点分别代入z=ax+y,
组成不等式组1≤3a,2a+2≤3a,a≤3a.
解得a≥2,
所以实数a的取值范围是[2,+∞).
故选:A.
点评 本题考查了线性规划的应用问题,是中档题.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2cos2x>1 | B. | $\frac{{x}^{4}}{si{n}^{2}x}$>$\frac{3}{4}$ | C. | x2+cos2x>1 | D. | x4-sin2x>$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?m∈R曲线C的焦距都为2 | B. | ?m∈R曲线C的焦距都不为2 | ||
| C. | ?m∈R曲线C的焦距不为2 | D. | ?m∈R曲线C的焦距不都为2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com