Question

5．如图，在多面体ABCDE中，CD和BE都垂直于平面ABC，且∠ACB=90°，AB=4，BE=1，CD=3，DE=2$\sqrt{2}$．
（Ⅰ）求证：BE∥平面ACD；
（Ⅱ）求多面体ABCDE的体积．

Answer 1

分析 （Ⅰ）证明BE∥CD，利用线面平行的判定即可证明BE∥平面ACD；
（Ⅱ）在平面BCDE内过点E作EF∥BC，交CD于点F，证明四边形BCDE是直角梯形，AC⊥平面DCBE，即可求多面体ABCDE的体积．

解答 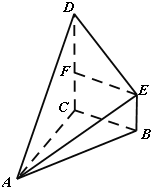（Ⅰ）证明：因为CD和BE都垂直于平面ABC，所以BE∥CD，
又CD?平面ACD，BE?平面ACD，
所以BE∥平面ACD． …（5分）
（Ⅱ）解：因为CD和BE都垂直于平面ABC，所以BE∥CD，
则四边形BCDE是直角梯形，…（6分）
在平面BCDE内过点E作EF∥BC，交CD于点F，
因为BE=1，CD=3，DE=2$\sqrt{2}$，…（7分）
在直角三角形DEF中，EF=2，
所以BC=EF=2，…（8分）
在直角三角形ABC中，AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=2$\sqrt{3}$，…（9分）
因为AC⊥BC，AC⊥DC，所以AC⊥平面DCBE，
而四边形BCDE的面积S=$\frac{1}{2}$（BE+CD）•BC=4，…（10分）
因此多面体ABCDE的体积为V=$\frac{1}{3}S•AC$=$\frac{8}{3}\sqrt{3}$．  …（12分）

点评 本题考查空间直线与平面之间的位置关系，线面平行，体积等知识，高考必考内容，考查空间想象能力和逻辑思维推理能力．