

分析 本题是直观图和三视图的综合分析题,要抓住M是A′B的中点,N是棱B′C′上的任意一点(含顶点)就是动点,从三视图抓住直观图的特征,结合下情况分别判断即可得答案.
解答 解:①M连接AB中点E,N连接BC中点F,得到MNFE平行于平面ACC′A′,面面平行即可得到线面平行,故①正确;
②M连接A′C中点G,连接C′G,A′C⊥平面MNC′G.∴MN⊥A′C,故②正确;
③三棱锥N-A′BC的体积为${V}_{N-{A}^{′}BC}$=$\frac{1}{3}$•S△BCA′•MB′=$\frac{1}{3}×\frac{1}{2}$•CA′•BC•MB′=$\frac{{a}^{3}}{6}$,故③正确;
④由三视图可知:此多面体是正方体切割下来了的,M是A′B的中点(空间对角线中点),是正方体中心,∴点M是该多面体外接球的球心.故④正确.
∴正确的是①②③④.
故答案为:①②③④.
点评 本题考查了棱锥、棱柱、棱台的体积,考查了直观图和三视图的关系,通过三视图抓住直观图的特征,线面垂直的判定和性质,遇中点找中点的思想.考虑补形来确定球心.考查空间想象能力,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
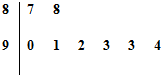 若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )| A. | 91、5 | B. | 91、5.5 | C. | 92、5.5 | D. | 92、5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{2}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2 | B. | ab | C. | $a\sqrt{{a^2}-{b^2}}$ | D. | $b\sqrt{{a^2}-{b^2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0)∪(0,+∞) | B. | [-1,0)∪(0,+∞) | C. | (-1,+∞) | D. | [-1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com