
分析 (1)化简函数,根据正弦函数的性质,在$x∈[{\frac{π}{4},\frac{π}{2}}]$上时,求出f(x)内层函数的范围,求解其最值.
(2)求出C角的大小,利用向量共线,求出A,B的关系,利用三角形内角和定理和正余弦定理即可求解.
解答 解:函数f(x)=$\sqrt{3}sinxcosx-{cos^2}x+\frac{1}{2}$.
化简得:f(x)=$\frac{\sqrt{3}}{2}$sin2x-($\frac{1}{2}$+$\frac{1}{2}$cos2x)+$\frac{1}{2}$
=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$cos2x
=sin(2x-$\frac{π}{6}$)
(1)∵$x∈[{\frac{π}{4},\frac{π}{2}}]$,
∴$2x-\frac{π}{6}∈[{\frac{π}{3},\frac{5π}{6}}]$.
当2x-$\frac{π}{6}$=$\frac{π}{2}$时,函数f(x)取得最大值为:1;
当2x-$\frac{π}{6}$=$\frac{5π}{6}$时,函数f(x)取得最小值为:$\frac{1}{2}$;
∴函数f(x)在$x∈[{\frac{π}{4},\frac{π}{2}}]$上的最值分别为:f(x)max=1,$f(x)_{min'}=\frac{1}{2}$.
(2)由题意:c=$\sqrt{7}$,f(C)=1,
则有:f(C)=sin(2C-$\frac{π}{6}$)=1
解得:C=$\frac{π}{3}$
又∵向量$\overrightarrow m=(1,sinA),\overrightarrow n=(3,sinB)$共线,
则有:sinA•sinB=3
由正弦定理,可得ab=3,b=$\frac{3}{a}$
由余弦定理:$cosC=\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$
⇒$cos\frac{π}{3}=\frac{{a}^{2}+\frac{9}{{a}^{2}}-7}{6}$
解得:a=1,
∵ab=3,
∴b=3
故a,b的值分别为1,3.
点评 本题考查了三角函数的化解能力和性质的运用,同时考查了正余弦定理的运用能力.属于中档题.


科目:高中数学 来源: 题型:选择题
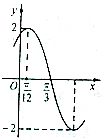
| A. | 函数f(x)的最小正周期为2π | |
| B. | 函数f(x)的图象关于点(-$\frac{5π}{12}$,0)对称 | |
| C. | 将函数f(x)的图象向左平移$\frac{π}{6}$个单位得到的函数图象关于y轴对称 | |
| D. | 函数f(x)的单调递增区间是[kπ+$\frac{7π}{12}$,kπ+$\frac{13π}{12}$](K∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤1 | B. | a≥1 | C. | a<1 | D. | a>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
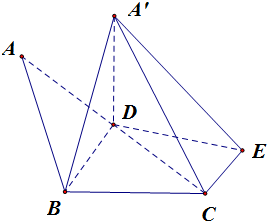 在△ABC中,AB=4,AC=4$\sqrt{2}$,∠BAC=45°,以AC的中线BD为折痕,将△ABD沿BD折起,如图所示,构成二面角A′-BD-C,在面BCD内作CE⊥CD,且$CE=\sqrt{2}$.
在△ABC中,AB=4,AC=4$\sqrt{2}$,∠BAC=45°,以AC的中线BD为折痕,将△ABD沿BD折起,如图所示,构成二面角A′-BD-C,在面BCD内作CE⊥CD,且$CE=\sqrt{2}$. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com