
已知命题p:方程a2x2+ax-2=0在[-1,1]上有解;命题q:只有一个实数x满足不等式x2+2ax+2a≤0,若命题“p或q”是假命题,求实数a的取值范围.
科目:高中数学 来源: 题型:
把下列命题改写成“若p则q”的形式,并写出它们的逆命题、否命题、逆否命题.
(1) 正三角形的三个内角相等;
(2) 已知a、b、c、d是实数,若a=b,c=d,则a+c=b+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知命题p1:函数y=ln(x+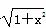 ),是奇函数,p2:函数y=x
),是奇函数,p2:函数y=x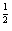 为偶函数,则下列四个命题:
为偶函数,则下列四个命题:
① p1∨p2;② p1∧p2;③ (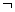 p1)∨p2;④ p1∧(
p1)∨p2;④ p1∧(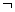 p2).
p2).
其中,真命题是________.(填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程,分别得到以下四个结论:①y与x负相关且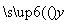 =2.347x-6.423;②y与x负相关且
=2.347x-6.423;②y与x负相关且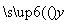 =-3.476x+5.648;③y与x正相关且
=-3.476x+5.648;③y与x正相关且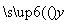 =5.437x+8.493;④y与x正相关且
=5.437x+8.493;④y与x正相关且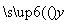 =-4.326x-4.578.
=-4.326x-4.578.
其中一定不正确的结论的序号是( )
A.①② B.②③
C.③④ D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com