
【题目】如图,在四棱锥![]() 中,底而
中,底而![]() 为菱形,且菱形
为菱形,且菱形![]() 所在的平面与
所在的平面与![]() 所在的平面相互垂直,
所在的平面相互垂直,![]() ,
,![]() ,
,![]() ,
,![]() .
.
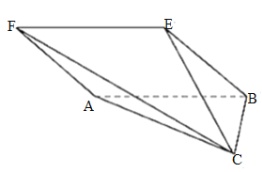
(1)求证:![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的最长侧棱的长.
的最长侧棱的长.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)在菱形![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,由此可证.
,由此可证.
(2)取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,由已知易得:
,由已知易得:![]() 是正三角形,
是正三角形,![]() ,进一步可证
,进一步可证![]() 平面
平面![]() ,由勾股定理可求出侧棱
,由勾股定理可求出侧棱![]() ,
,![]() ,
,![]() ,
,![]() 的长度,得到最长的是
的长度,得到最长的是![]() ,或可先判断CF最长,求解出长度即可.
,或可先判断CF最长,求解出长度即可.
(1)在菱形![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
∴![]() 平面
平面![]() .
.
(2)方法一:取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,
,
由已知易得:![]() 是正三角形,∴
是正三角形,∴![]() .
.
又∴平面![]() 平面
平面![]() 且交线为
且交线为![]() ,∴
,∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ,
,![]() ,
,
在菱形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
显然在侧棱![]() ,
,![]() ,
,![]() ,
,![]() 中最长的是
中最长的是![]() .
.
∴四棱锥![]() 的最长侧棱的长为
的最长侧棱的长为![]() .
.
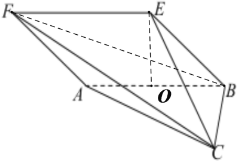
方法二:取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,
,
由已知易得:![]() 是正三角形,∴
是正三角形,∴![]() ,
,
又∵平面![]() 平面
平面![]() 且交线为
且交线为![]() ,∴
,∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() .
.
又![]() ,
,![]() 平面
平面![]() ∴
∴![]() ,
,![]() .
.
在菱形![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() 最长.
最长.
在![]() 中,
中,![]() .
.
∴四棱锥![]() 的最长侧棱的长为
的最长侧棱的长为![]() .
.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】太极是中国古代的哲学术语,意为派生万物的本源.太极图是以黑白两个鱼形纹组成的圆形图案,俗称阴阳鱼.太极图形象化地表达了阴阳轮转,相反相成是万物生成变化根源的哲理.太极图形展现了一种互相转化,相对统一的形式美.按照太极图的构图方法,在平面直角坐标系中,圆![]() 被
被![]() 的图象分割为两个对称的鱼形图案,图中的两个一黑一白的小圆通常称为“鱼眼”,已知小圆的半径均为
的图象分割为两个对称的鱼形图案,图中的两个一黑一白的小圆通常称为“鱼眼”,已知小圆的半径均为![]() ,现在大圆内随机投放一点,则此点投放到“鱼眼”部分的概率为( )
,现在大圆内随机投放一点,则此点投放到“鱼眼”部分的概率为( )
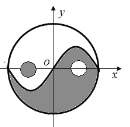
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济全球化、信息化的发展,企业之间的竞争从资源的争夺转向人才的竞争,吸引、留住培养和用好人才成为人力资源管理的战略目标和紧迫任务,在此背景下,某信息网站在15个城市中对刚毕业的大学生的月平均收入薪资和月平均期望薪资做了调查,数据如下图所示.
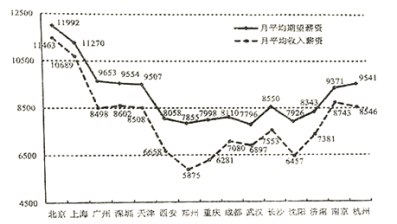
(Ⅰ)若某大学毕业生从这15座城市中随机选择一座城市就业,求该生选中月平均收入薪资高于8500元的城市的概率;
(Ⅱ)若从月平均收入薪资与月平均期望薪资之差高于1100元的城市中随机选择2座城市,求这2座城市的月平均期望薪资都低于8500元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地自2014年至2019年每年年初统计所得的人口数量如表所示:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
人数(单位:千人) | 2082 | 2135 | 2203 | 2276 | 2339 | 2385 |
(1)根据表中的数据判断从2014年到2019年哪个跨年度的人口增长数量最大?并描述该地人口数量的变化趋势;
(2)研究人员用函数![]() 拟合该地的人口数量,其中
拟合该地的人口数量,其中![]() 的单位是年,2014年年初对应时刻
的单位是年,2014年年初对应时刻![]() ,
,![]() 的单位是千人,经计算可得
的单位是千人,经计算可得![]() ,请解释
,请解释![]() 的实际意义.
的实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为了响应国家政策,我市环保部门对市民进行了一次环境保护知识的网络问卷调查,每位市民仅有一次参加机会,通过随机抽样,得到参与问卷调查的50人的得分(满分:100分)数据,统计结果如表所示:
组别 |
|
|
|
|
|
|
男 | 1 | 2 | 2 | 10 | 9 | 6 |
女 | 0 | 5 | 5 | 5 | 3 | 2 |
若规定问卷得分不低于70分的市民称为“环境保护关注者”,则上图中表格可得![]() 列联表如下:
列联表如下:
非“环境保护关注者” | 是“环境保护关注者” | 合计 | |
男 | 5 | 25 | 30 |
女 | 10 | 10 | 20 |
合计 | 15 | 35 | 50 |
(1)请完成上述![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“环境保护关注者”与性别有关?
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“环境保护关注者”与性别有关?
(2)若问卷得分不低于80分的人称为“环境保护达人”,现在从本次调查的“环境保护达人”中利用分层抽样的方法抽取4名市民参与环保知识问答,再从这4名市民中随机抽取2人参与座谈会,求抽取的2名市民中,既有男“环境保护达人”又有女“环境保护达人”的概率.
附表及公式: ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】推进垃圾分类处理,是落实绿色发展理念的必然选择,也是打赢污染防治攻坚战的重要环节.为了解居民对垃圾分类的了解程度,某社区居委会随机抽取1000名社区居民参与问卷测试,并将问卷得分绘制频率分布表如下:
得分 |
|
|
|
|
|
|
|
男性人数 | 40 | 90 | 120 | 130 | 110 | 60 | 30 |
女性人数 | 20 | 50 | 80 | 110 | 100 | 40 | 20 |
(1)从该社区随机抽取一名居民参与问卷测试,试估计其得分不低于60分的概率;
(2)将居民对垃圾分类的了解程度分为“比较了解“(得分不低于60分)和“不太了解”(得分低于60分)两类,完成![]() 列联表,并判断是否有95%的把握认为“居民对垃圾分类的了解程度”与“性别”有关?
列联表,并判断是否有95%的把握认为“居民对垃圾分类的了解程度”与“性别”有关?
不太了解 | 比较了解 | |
男性 | ||
女性 |
(3)从参与问卷测试且得分不低于80分的居民中,按照性别进行分层抽样,共抽取10人,连同![]() 名男性调查员一起组成3个环保宜传队.若从这
名男性调查员一起组成3个环保宜传队.若从这![]() 中随机抽取3人作为队长,且男性队长人数占的期望不小于2.求
中随机抽取3人作为队长,且男性队长人数占的期望不小于2.求![]() 的最小值.
的最小值.
附:![]()
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名同学参加一项射击比赛游戏,其中任何一人每射击一次击中目标得2分,未击中目标得0分.若甲、乙两人射击的命中率分别为![]() 和
和![]() ,且甲、乙两人各射击一次得分之和为2的概率为
,且甲、乙两人各射击一次得分之和为2的概率为![]() .假设甲、乙两人射击互不影响,则
.假设甲、乙两人射击互不影响,则![]() 值为( )
值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com