
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据折叠前后线段、角的变化情况,用线面平行、面面垂直的判定定理和性质定理进行判定.
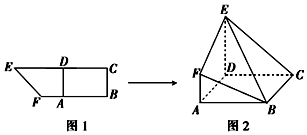
解答 解:解:对于①,在图2中记AC与BD的交点(中点)为O,取BE的中点为M,连结MO,易证得四边形AOMF为平行四边形,即AC∥FM,∴AC∥平面BEF,故①正确;
对于②,如果四点共面,则Y由BC∥平面ADEF⇒BC∥EF∥AB⇒BC=EF,与已知矛盾,故②正确;
对于③,在梯形ADEF中,易得EF⊥FD,又EF⊥CF,∴EF⊥平面CDF,即有CD⊥EF,∴CD⊥平面ADEF,则平面ADEF⊥平面ABCD,故③正确;
对于④,延长AF至G使得AF=FG,连结BG、EG,易得平面BCE⊥平面ABF,过F作FN⊥BG于N,则FN⊥平面BCE.若平面BCE⊥平面BEF,则过F作直线与平面BCE垂直,其垂足在BE上,矛盾,故④错误.
故选:B
点评 本题考查了线面平行、面面垂直的判定定理和性质定理的运用.考查了学生的空间想象能力和推理能力,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com