
分析 根据一元二次不等式的解和对应的一元二次方程实数根的关系即可求得a=2,从而得到f(x)=x2-4x+3,令t=x2-4x+3,从而f(t)<0的解为1<t<3,从而得到1<x2-4x+3<3,解该一元二次不等式即得不等式f[f(x)]<0的解集.
解答 解:根据题意,x=1,3是方程x2-2ax+a2-1=0的两个实根;
∴$\left\{\begin{array}{l}{1+3=2a}\\{1•3={a}^{2}-1}\end{array}\right.$;
解得,a=2;
f(x)=x2-4x+3;
令f(x)=t,由f[f(x)]<0得f(t)<0;
根据已知,1<t<3;
∴1<x2-4x+3<3;
解得,0$<x<2-\sqrt{2}$,或$2+\sqrt{2}<x<4$;
∴f[f(x)]<0的解集为(0,2-$\sqrt{2}$)∪(2+$\sqrt{2}$,4).
故答案为:$(0,2-\sqrt{2})∪(2+\sqrt{2},4)$.
点评 考查一元二次不等式的解和对应的一元二次方程实数根的关系,韦达定理,换元法解不等式,解一元二次不等式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在几何体ABCDN中,CD⊥平面ABC,DC∥AN,CD=2AN=4,又AB=AC=BC=2,点P是BD上的动点(与B、D两点不重合).
如图,在几何体ABCDN中,CD⊥平面ABC,DC∥AN,CD=2AN=4,又AB=AC=BC=2,点P是BD上的动点(与B、D两点不重合).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
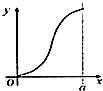 如图,有四个平面图形分别是三角形、平行四边形、直角梯形、圆.垂直于x轴的直线l:x=t(0≤t≤a)经过原点O向右平行移动,l在移动过程中扫过平面图形的面积为y(图中阴影部分),若函数y=f(t)的大致图象如图,那么平面图形的形状不可能是( )
如图,有四个平面图形分别是三角形、平行四边形、直角梯形、圆.垂直于x轴的直线l:x=t(0≤t≤a)经过原点O向右平行移动,l在移动过程中扫过平面图形的面积为y(图中阴影部分),若函数y=f(t)的大致图象如图,那么平面图形的形状不可能是( )| A. | 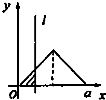 | B. | 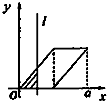 | C. | 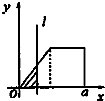 | D. | 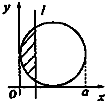 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com