
 设点P在曲线y=$\frac{1}{2}$x2上,从原点向A(2,2)移动,如果直线OP,曲线y=$\frac{1}{2}$x2及直线x=2所围成的阴影部分面积分别记为S1、S2.
设点P在曲线y=$\frac{1}{2}$x2上,从原点向A(2,2)移动,如果直线OP,曲线y=$\frac{1}{2}$x2及直线x=2所围成的阴影部分面积分别记为S1、S2.分析 (Ⅰ)可考虑用定积分求两曲线围成的封闭图形面积,直线OP的方程为y=$\frac{1}{2}$tx,则S1为直线OP与曲线y=$\frac{1}{2}$x2当x∈(0,t)时所围面积,所以,S1=∫0t($\frac{1}{2}$tx-$\frac{1}{2}$x2)dx,S2为直线OP与曲线y=$\frac{1}{2}$x2当x∈(t,2)时所围面积,所以S2=∫t2($\frac{1}{2}$x2-$\frac{1}{2}$tx)dx,再根据S1=S2就可求出t值.
(Ⅱ)由(Ⅰ)可求当S1+S2,化简后,为t的三次函数,再利用导数求最小值,以及相应的x值,就可求出P点坐标为多少时,S1+S2有最小值.
解答 解:(Ⅰ)设点p的横坐标为t(0<t<2),
则P点的坐标为(t,$\frac{1}{2}$t2),
直线OP的方程为y=$\frac{1}{2}$tx,
s1=${∫}_{0}^{t}$($\frac{1}{2}$tx-$\frac{1}{2}$x2)dx=$\frac{1}{12}$t3,S2=${∫}_{t}^{2}$($\frac{1}{2}$x2-$\frac{1}{2}$tx)dx=$\frac{1}{12}$t3-t+$\frac{4}{3}$,
因为S1=S2,所以t=$\frac{4}{3}$,点P的坐标为($\frac{4}{3}$,$\frac{8}{9}$).
(Ⅱ)S=S1+S2=$\frac{1}{12}$t3+$\frac{1}{12}$t3-t+$\frac{4}{3}$=$\frac{1}{6}$t3-t+$\frac{4}{3}$,
S′=$\frac{1}{2}$t2-1,令S′=0,得$\frac{1}{2}$t2-1=0,∴t=$\sqrt{2}$,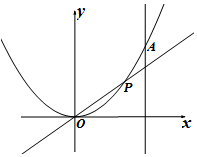
因为9<t<$\sqrt{2}$时,S′<0;$\sqrt{2}$<t<2时,S′>0,
所以,当t=$\sqrt{2}$时,Smin=$\frac{4-2\sqrt{2}}{3}$,
P点的坐标为($\sqrt{2}$,1).
点评 本题考查了用定积分求两曲线所围图形面积,以及导数求最值,做题时应认真分析.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${∫}_{0}^{1}$xdx | B. | ${∫}_{0}^{1}$$\frac{1}{x}$dx | C. | ${∫}_{0}^{1}$$\sqrt{x}$dx | D. | ${∫}_{0}^{1}$x2dx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>|b|,则a2>b2 | B. | 若|a|>b,则a2>b2 | ||
| C. | 若a≥b,则a2≥b2 | D. | 若a>b,c>d,则ac>bd |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,抛物线形拱桥的顶点距水面2米时,测得拱桥内水面宽为12米,当水面下降1米后,拱桥内水面宽度是( )
如图,抛物线形拱桥的顶点距水面2米时,测得拱桥内水面宽为12米,当水面下降1米后,拱桥内水面宽度是( )| A. | 6$\sqrt{2}$米 | B. | 6$\sqrt{6}$米 | C. | 3$\sqrt{2}$米 | D. | 3$\sqrt{6}$米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com