
| A. | $y={({\frac{1}{2}})^{|x|}}$ | B. | y=|log2(-x)| | C. | $y={x^{\frac{2}{3}}}$ | D. | y=sin|x| |
分析 根据基本函数的性质依次判断即可得答案.
解答 解:对于A:根据指数函数的性质,$y=(\frac{1}{2})^{|x|}$的图象是y=$(\frac{1}{2})^{x}$图象把y轴的右边图象翻折后得左边图象,在(-∞,0)上单调递增函数,∴A不对.
对于B:根据图象,y=|log2(-x)|,在(-∞,-1)是减函数,(-1,0)是增函数,∴B不对.
对于C:根据幂函数的性质可知:$y={x}^{\frac{2}{3}}$是偶函数,指数$\frac{2}{3}>0$,(0,+∞)是增函数.(-∞,0)上单调递减.∴C对.
对于D:根据正弦函数的性质可知:y=sin|x|的图象是由sinx在y轴的右边图象翻折后得左边图象.
故选:C.
点评 本题考查了基本函数的图象和性质,平移问题转化,翻折问题,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
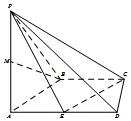 如图,在四棱锥P-ABCD中,AD∥BC,BC⊥CD,点P在底面ABCD上的射影为A,BC=CD=$\frac{1}{2}$AD=1,E为棱AD的中点,M为棱PA的中点.
如图,在四棱锥P-ABCD中,AD∥BC,BC⊥CD,点P在底面ABCD上的射影为A,BC=CD=$\frac{1}{2}$AD=1,E为棱AD的中点,M为棱PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 测试指标 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 芯片数量(件) | 8 | 22 | 45 | 37 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com