
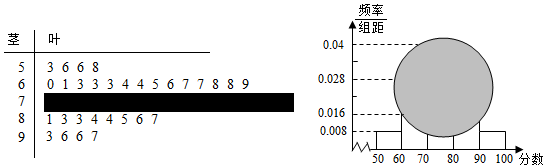
分析 (I)由茎叶图可知,分数在[50,60)上的频数,频率,进而确定参赛人数,从而可得结论;
(II)确定被抽中的成绩位于[70,80)分数段的学生人数X所有取值,求出相应概率,即可求分布列与期望
解答 解:(I)由茎叶图可知,分数在[50,60)上的频数为4人,
频率为0.008×10=0.08,
参赛人数为$\frac{4}{0.08}$=50人,
分数在[70,80)上的频数等于50-(4+14+8+4)=20人.
(II)按分层抽样的原理,三个分数段抽样数之比等于相应频率之比.
又[70,80),[80,90)分数段频率之比等于5:2,
由此可抽出样本中分数在[70,80)的有5人,分数在[80,90)的有2人,
从中任选2人共有${C}_{7}^{2}$=21种选法,
记交流的学生中,成绩位于[70,80)分数的人恰有一人为事件A.
则A中共有:${C}_{5}^{1}{C}_{2}^{1}$=10种情况,
故交流的学生中,成绩位于[70,80)分数的人恰有一人的概率P=$\frac{10}{21}$.
点评 本题考查概率知识的应用,考查概率的计算,考查频率分布直方图和茎叶图,分层抽样,是概率和统计的综合应用,难度中档.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.08 | B. | 0.42 | C. | 0.84 | D. | 0.16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{13}}{4}$ | B. | $\frac{\sqrt{13}}{2}$ | C. | $\frac{\sqrt{53}}{4}$ | D. | $\frac{\sqrt{53}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在棱长为1的正方体ABCD-A1B1C1D1中,E为线段B1C的中点,F是棱C1D1上的动点,若点P为线段BD1上的动点,则PE+PF的最小值为( )
在棱长为1的正方体ABCD-A1B1C1D1中,E为线段B1C的中点,F是棱C1D1上的动点,若点P为线段BD1上的动点,则PE+PF的最小值为( )| A. | $\frac{1+\sqrt{2}}{2}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{5\sqrt{2}}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com