
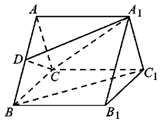
 如图,在三棱柱ABC-A1B1C1中,底面△ABC是等边三角形,侧面AA1B1B为正方形,且AA1⊥平面ABC,D为线段AB上的一点.
如图,在三棱柱ABC-A1B1C1中,底面△ABC是等边三角形,侧面AA1B1B为正方形,且AA1⊥平面ABC,D为线段AB上的一点.分析 (Ⅰ)D为AB的中点,理由如下:连接AC1,交A1C于点E,可知E为AC1的中点,连接DE,利用线面平行的性质定理、三角形中平行线的性质即可得出.
(Ⅱ)不妨设AB=2,分别取BC,B1C1的中点O,O1,连接AO,OO1,可知OB,OO1,OA两两互相垂直,建立如图的空间直角坐标系O-xyz.利用线面垂直的性质定理、向量垂直与数量积的关系可得:平面A1CD的法向量$\overrightarrow{m}$,又平面BCC1的一个法向量$\overrightarrow{n}$=(0,0,1),利用向量夹角公式即可得出.
解答 解:(Ⅰ)D为AB的中点,理由如下:
连接AC1,交A1C于点E,可知E为AC1的中点,连接DE,
因为BC1∥平面A1CD,
平面ABC1∩平面A1CD=DE,
所以BC1∥DE,
故D为AB的中点.(4分)
(Ⅱ)不妨设AB=2,分别取BC,B1C1的中点O,O1,连接AO,OO1,可知OB,OO1,OA两两互相垂直,建立如图的空间直角坐标系O-xyz.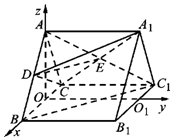
知$C(-1,0,0),D(\frac{1}{2},0,\frac{{\sqrt{3}}}{2}),{A_1}(0,2,\sqrt{3})$,
则$\overrightarrow{CD}=(\frac{3}{2},0,\frac{{\sqrt{3}}}{2})$,$\overrightarrow{C{A_1}}=(1,2,\sqrt{3})$,
设面A1CD的法向量m=(x,y,z),
由$\left\{\begin{array}{l}m•\overrightarrow{CD}=0\\ m•\overrightarrow{C{A_1}}=0\end{array}\right.$得$\left\{\begin{array}{l}\frac{3}{2}x+\frac{{\sqrt{3}}}{2}z=0\\ x+2y+\sqrt{3}z=0\end{array}\right.$
令x=1,得A1CD的一个法向量为$m=(1,1,-\sqrt{3})$,
又平面BCC1的一个法向量n=(0,0,1),
设二面角A1D-C-BC1的平面角为α,
则$cosα=|{cos<m,n>}|=\frac{{|{m•n}|}}{|m|•|n|}=\frac{{\sqrt{15}}}{5}$.
即该二面角的余弦值为$\frac{{\sqrt{15}}}{5}$.(12分)
点评 本题考查了线面垂直与平行的判定与性质定理、向量垂直与数量积的关系、平面法向量的应用、向量夹角公式、三角形中位线定理,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{5}{4}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
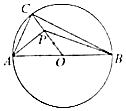 如图,AB为圆O的直径且AB=4,C为圆上不同于A、B的任意一点,若P为半径OC上的动点,则($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PC}$的最小值是( )
如图,AB为圆O的直径且AB=4,C为圆上不同于A、B的任意一点,若P为半径OC上的动点,则($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PC}$的最小值是( )| A. | -4 | B. | -3 | C. | -2 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤-1或x≥3} | B. | {x|x<1或x≥3} | C. | {x|x≤1} | D. | {x|x≤-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<3} | B. | {x|-1<x<3} | C. | {x|-1<x<0或0<x<3} | D. | {x|-1<x<0或1<x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
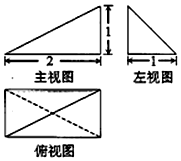
| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | $2\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com