
分析 (1)代入可得f(x)=|x-3|-x,去绝对值,分类讨论即可;
(2)整理不等式得|x+1|+|x-a|>1恒成立,只需求左式的最小值,利用绝对值不等式性质可解.
解答 解:(1)当a=3时,
f(x)=|x-3|-x,
当x≥3时,f(x)=-3.
当x<3时,f(x)=-2x+3,
∴f(x)>f(3)=-3,
∴f(x)的值域为[-3,+∞);
(2)g(x)+x>1-f(x)恒成立,
∴|x+1|+|x-a|>1恒成立,
∵|x+1|+|x-a|≥|x+1-(x-a)|=|a+1|,
∴|a+1|>1,
∴a>0或a<-2.
点评 考查了绝对值函数和绝对值不等式性质,恒成立问题的转换.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
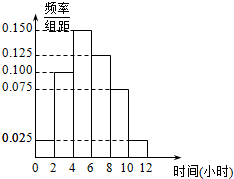 某高校共有学生15 000人,其中男生10 500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
某高校共有学生15 000人,其中男生10 500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com