
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-1,0)∪(0,1) | D. | (-∞,-1)∪(1,+∞) |
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{10}{21}$ | B. | $\frac{20}{21}$ | C. | $\frac{10}{19}$ | D. | $\frac{20}{19}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
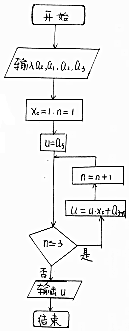 如图程序框图的算法思路来源于我国古代数学名著《数学九章》中的“秦九韶算法”求多项式的值.执行程序框图,若输入a0=1,a1=1,a2=0,a3=-1,则输出的u的值为( )
如图程序框图的算法思路来源于我国古代数学名著《数学九章》中的“秦九韶算法”求多项式的值.执行程序框图,若输入a0=1,a1=1,a2=0,a3=-1,则输出的u的值为( )| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 过直线外一点有且只有一条直线与已知直线平行 | |
| B. | 不公线的三个点确定一个平面 | |
| C. | 如果两条直线垂直于同一条直线,那么这两条直线平行 | |
| D. | 如果两个平面垂直于同一个平面,那么这两个平面可能互相垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
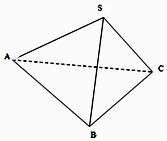 如图,已知三棱锥S-ABC中,SA=SB=CA=CB=$\sqrt{3}$,AB=2,SC=$\sqrt{2}$,则二面角S-AB-C的平面角的大小为( )
如图,已知三棱锥S-ABC中,SA=SB=CA=CB=$\sqrt{3}$,AB=2,SC=$\sqrt{2}$,则二面角S-AB-C的平面角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | lnx0 | B. | $ln\sqrt{x_0}$ | C. | ln(lnx0) | D. | ${(ln{x_0})^2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com