
���� �⣺����f��x����ͼ����ͼ��ʾ��
���ڢ٣�f��1��=2��f��f��1����=f��2��=$\frac{3}{2}$��f��3��=$\frac{4}{3}$����
���ڢڣ�x��1ʱ��f�䣨x��=-$\frac{1}{{x}^{2}}$=-$\frac{1}{3}$��⇒x=$\sqrt{3}$����
���ڢۣ�����ͼ�ο��жϣ�
���ڢܣ���x�ʣ�0��+�ޣ�ʱ��1��f��x����2�����ж�
��� �⣺����f��x����ͼ����ͼ��ʾ��
���ڢ٣�f��1��=2��f��f��1����=f��2��=$\frac{3}{2}$��f��3��=$\frac{4}{3}$���ʢ���ȷ��
���ڢڣ�x��1ʱ��f�䣨x��=-$\frac{1}{{x}^{2}}$=-$\frac{1}{3}$��⇒x=$\sqrt{3}$���ʢ���ȷ��
���ڢۣ�����ͼ�ο��жϢ���ȷ��
���ڢܣ�x�ʣ�0��+�ޣ�ʱ��1��f��x����2��
��?x1��x2�ʣ�0��+�ޣ���|f��x1��-f��x2��|��1��ȷ
�ʴ�Ϊ���٢ڢۢ�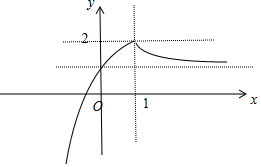
���� ���⿼���˺�����ͼ�������ʣ����ν��˼�롢ת��˼�룬�����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
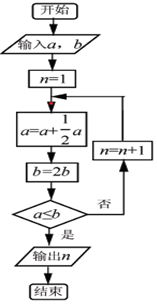 ִ����ͼ��ʾ�ij����ͼ���������a=16��b=4���������n=��������
ִ����ͼ��ʾ�ij����ͼ���������a=16��b=4���������n=��������| A�� | 4 | B�� | 5 | C�� | 6 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 17 | B�� | 14 | C�� | 13 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=x3 | B�� | y=2|x| | C�� | y=-x2 | D�� | y=log3��-x�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{5}}{2}$ | B�� | $\sqrt{2}$ | C�� | $\frac{2\sqrt{3}}{3}$ | D�� | $\sqrt{10}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{3}+1}}{2}$ | B�� | $\frac{3}{2}$ | C�� | $\sqrt{3}$ | D�� | $2\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
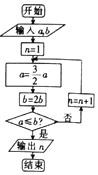 ��������ѧ���ɡ����������⣺���ɳ���ߣ������ߣ������룬�����Ա���������ն����ȡ�����λ�����˼�ǣ���������߳����������߳�����ÿ������ǰһ�쳤�ȵ�һ�룬��ÿ������ǰһ�쳤�ȵ�����������Ϊ���о�������⣬��a�����ɳ�����b�������������ͼ��ʾ�ij����ͼ�������a��b��ֵ�ֱ�Ϊ5��2���������n��ֵΪ��������
��������ѧ���ɡ����������⣺���ɳ���ߣ������ߣ������룬�����Ա���������ն����ȡ�����λ�����˼�ǣ���������߳����������߳�����ÿ������ǰһ�쳤�ȵ�һ�룬��ÿ������ǰһ�쳤�ȵ�����������Ϊ���о�������⣬��a�����ɳ�����b�������������ͼ��ʾ�ij����ͼ�������a��b��ֵ�ֱ�Ϊ5��2���������n��ֵΪ��������| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com