
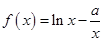 ,其中
,其中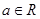 .
.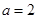 时,求函数
时,求函数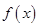 的图象在点
的图象在点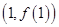 处的切线方程;
处的切线方程;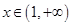 ,都有
,都有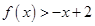 ,求
,求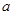 的取值范围.
的取值范围. 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:高中数学 来源:不详 题型:解答题
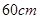 的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?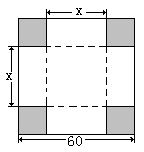
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
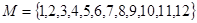 ,以下命题正确的序号是 .
,以下命题正确的序号是 .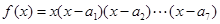 ,其中
,其中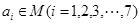 ,那么
,那么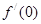 的最大值为
的最大值为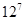 。
。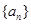 满足首项
满足首项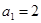 ,
,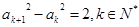 ,当
,当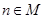 且
且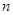 最大时,数列
最大时,数列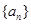 有2048个。
有2048个。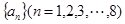 满足
满足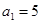 ,
,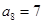 ,
,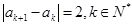 ,如果数列
,如果数列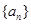 中的每一项都是集合M的元素,则符合这些条件的不同数列
中的每一项都是集合M的元素,则符合这些条件的不同数列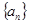 一共有33个。
一共有33个。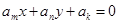 ,其中
,其中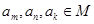 ,而且
,而且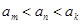 ,则一共可以得到不同的直线196条。
,则一共可以得到不同的直线196条。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
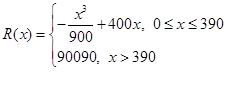 ,则当总利润最大时,每年生产产品的单位数是( )
,则当总利润最大时,每年生产产品的单位数是( )| A.150 |
| B.200 |
| C.250 |
| D.300 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com