
选修4-5:不等式选讲(本小题满分10分)
设函数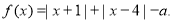
(1)当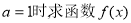 的最小值;
的最小值;
(2)若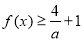 对任意的实数
对任意的实数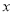 恒成立,求实数
恒成立,求实数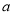 的取值范围.
的取值范围.
【解析】
(1)当a=1时,f(x)=|x+1|+|x-4|-1≥|(x+1)-(x-4)|-1=5-1=4.
所以函数f(x)的最小值为4.
(2)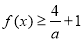 对任意的实数x恒成立|x+1|+|x-4|-1≥a+
对任意的实数x恒成立|x+1|+|x-4|-1≥a+ 对任意的实数x恒成立a+
对任意的实数x恒成立a+ ≤4对任意实数x恒成立.
≤4对任意实数x恒成立.
当a<0时,上式显然成立;
当a>0时,a+ ≥4,当且仅当a=2时上式取等号,
≥4,当且仅当a=2时上式取等号,
综上,实数a的取值范围为(-∞,0)∪{2}.
【解析】
试题分析:(1)当a=1时,利用绝对值不等式的性质即可求得最小值;(2)若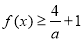 对任意的实数
对任意的实数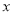 恒成立,即求f(x)的最小值,对a进行分类讨论可求a的取值范围
恒成立,即求f(x)的最小值,对a进行分类讨论可求a的取值范围
考点:不等式的解法及应用
点评:本题考查绝对值函数、基本不等式以及恒成立问题,考查分类讨论思想,恒成立问题一般转化为函数最值问题解决.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源:2014-2015学年广东省肇庆市高二上学期期末考试理科数学试卷(解析版) 题型:选择题
已知双曲线与抛物线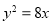 有公共的焦点,且双曲线的离心率为2,则该双曲线的标准方程为
有公共的焦点,且双曲线的离心率为2,则该双曲线的标准方程为
A.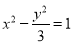 B.
B.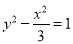 C.
C.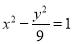 D.
D.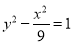
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省天水市高三一轮复习基础知识检测文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4—4;坐标系与参数方程
已知直线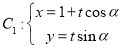 (
( 为参数),
为参数), .
.
(1)当 时,求
时,求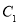 与
与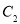 的交点坐标;
的交点坐标;
(2)以坐标原点 为圆心的圆与
为圆心的圆与 相切,切点为
相切,切点为 ,
,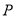 为
为 的中点,当
的中点,当 变化时,求
变化时,求 点的轨迹的参数方程,并指出它是什么曲线.
点的轨迹的参数方程,并指出它是什么曲线.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省天水市高三一轮复习基础知识检测文科数学试卷(解析版) 题型:填空题
已知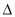 ABC的三个顶点在以O为球心的球面上,且
ABC的三个顶点在以O为球心的球面上,且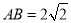 ,BC=1,AC=3,三棱锥O-ABC的体积为
,BC=1,AC=3,三棱锥O-ABC的体积为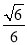 ,则球O的表面积为 .
,则球O的表面积为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高一上学期第三次月考数学试卷(解析版) 题型:解答题
(本小题满分12分,(1)小问5分,(2)小问7分)
已知函数 .
.
(1)设函数 ,若函数
,若函数 为偶函数,求实数
为偶函数,求实数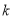 的值;
的值;
(2)当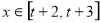 时,是否存在实数
时,是否存在实数 (其中
(其中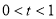 ),使得不等式
),使得不等式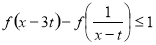 恒成立?若存在,求出
恒成立?若存在,求出 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高一上学期12月月考数学试卷(解析版) 题型:解答题
(本题满分12分)设函数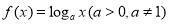 ,
,
(1)若不等式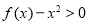 在
在 内恒成立,求
内恒成立,求 的取值范围;
的取值范围;
(2)判断是否存在大于1的实数 ,使得对任意
,使得对任意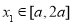 ,都有
,都有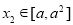 满足等式:
满足等式: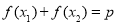 ,且满足该等式的常数
,且满足该等式的常数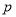 的取值唯一?若存在,求出所有符合条件的
的取值唯一?若存在,求出所有符合条件的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com