已知函数f(x)=aln(x+1)+(x+1)2
(1)讨论函数f(x)的单调性;
(2)当a>0时,若对任意x1x2∈(-1,+∞),都有f(x1-f(x2)|≥3|x1-x2|,求a的取值范围、
解:由题可知f(x)的定义域为(-1,+∞),
(i)当a≥0时,因为函数f(x)
1=aln(x+1)和f(x)
2=(x+1)
2在(-1,+∞)上均为增函数,
故f(x)=aln(x+1)+(x+1)
2在(-1,+∞)上均为增函数;
(ii)a<0时,f′(x)=
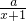
+2(x+1),
令f′(x)=0,得x
1=-1+
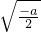
,x
2=-1-
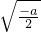
(舍),
当x变化时,f′(x)与f(x)的变化情况如下表:
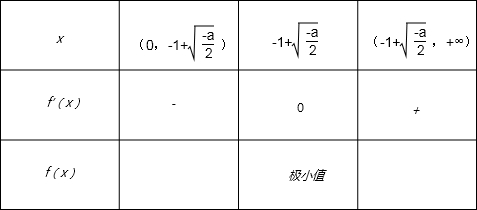
由表可知,f(x)的单调减区间为(0,-1+
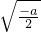
),f(x)的单调增区间为(-1+
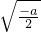
,+∞)
综上,当a≥0时,f(x)=aln(x+1)+(x+1)
2在(-1,+∞)上均为增函数,
当a<0时,f(x)的单调减区间为(0,-1+
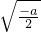
),f(x)的单调增区间为(-1+
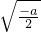
,+∞);
(2)不妨设x
1<x
2,则所证的式子化为:f(x
2)-f(x
1)≥3(x
2-x
1),即f(x
2)-3x
2≥f(x
1)-3x
1,
令F(x)=f(x)-3x=aln(x+1)+x
2-x+1,则F(x)在(-1,+∞)上为增函数.
即F'(x)=
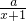
+2x-1≥0在(-1,+∞)上恒成立,因为x>-1,所以a≥-2x
2-x+1在(-1,+∞)上恒成立,
而二次函数-2x
2-x+1在(-∞,-

)上单调递增,在(-

,+∞)上单调递减,
故在(-1,+∞)上的最大值为-2(-
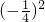
-(-

)+1=

,
所以a≥

,
故a的取值范围是[

,+∞].
分析:根据负数没有对数,得到函数f(x)的定义域,
(1)(i)当a大于等于0时,因为函数aln(x+1)与(x+1)
2在x大于等于-1时都为增函数,所以单调f(x)也为增函数;(ii)当a小于0时,求出f(x)的导函数,令导函数等于单调x的值,在函数定义域内由x的值讨论导函数的正负进而得到函数的单调区间,综上,分a大于等于0和a小于0两种情况写出函数的单调区间即可;
(2)设x
1小于x
2,把所证的式子化简,得到f(x
2)-3x
2≥f(x
1)-3x
1,令F(x)=f(x)-3x,进而单调F(x)在x大于-1为增函数,即导函数恒大于等于0,由导函数解出a大于等于一个二次函数,根据x的范围求出二次函数的最大值,即可得到a的取值范围.
点评:此题考查学生会利用导函数的正负确定函数的单调区间,掌握导数在最大值、最小值中的应用,掌握不等式恒成立时所满足的条件,考查了转化的数学思想,是一道中档题.

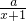 +2(x+1),
+2(x+1),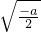 ,x2=-1-
,x2=-1-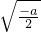 (舍),
(舍),
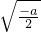 ),f(x)的单调增区间为(-1+
),f(x)的单调增区间为(-1+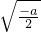 ,+∞)
,+∞)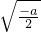 ),f(x)的单调增区间为(-1+
),f(x)的单调增区间为(-1+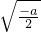 ,+∞);
,+∞);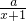 +2x-1≥0在(-1,+∞)上恒成立,因为x>-1,所以a≥-2x2-x+1在(-1,+∞)上恒成立,
+2x-1≥0在(-1,+∞)上恒成立,因为x>-1,所以a≥-2x2-x+1在(-1,+∞)上恒成立, )上单调递增,在(-
)上单调递增,在(- ,+∞)上单调递减,
,+∞)上单调递减,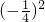 -(-
-(- )+1=
)+1= ,
, ,
, ,+∞].
,+∞].

 每课必练系列答案
每课必练系列答案