
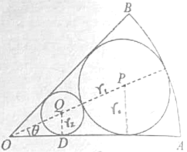
【题目】如图,在半径为常量![]() ,圆心角为变量
,圆心角为变量![]() 的扇形
的扇形![]() 内作一内切圆
内作一内切圆![]() ,再在扇形内作一个与扇形两半径相切并与圆
,再在扇形内作一个与扇形两半径相切并与圆![]() 外切的小圆
外切的小圆![]() ,设圆
,设圆![]() 的半径为
的半径为![]() ,则
,则![]() 的半径为
的半径为![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)求圆![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】端午佳节旌旗胜,龙舟竞渡展雄风.端午龙舟竞渡活动是我国的民间传统习俗,龙舟精神激发着汕尾海陆丰老区人民敢为人先、奋发有为的勇气.每年在粽叶飘香的端午节到来的前一天,汕尾市都将在美丽的品清湖畔举行龙舟锦标赛,他们将在这片碧蓝的品清湖上挥桨劈浪,奋勇争先,一往无前的龙舟精神,该活动也为市民提供了难得的视觉盛宴.某商家为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了6月2日至6月6日的白天平均气温![]() (℃)与该奶茶店的这种饮料销量
(℃)与该奶茶店的这种饮料销量![]() (杯),得到如下数据:
(杯),得到如下数据:
日期 | 6月2日 | 6月3日 | 6月4日 | 6月5日 | 6月6日 |
平均气温 | 27 | 29 | 31 | 30 | 33 |
销量 | 23 | 25 | 30 | 26 | 21 |
(1)先从这五组数据中抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出了![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;若气象台预报6月7日白天的平均气温为35℃,根据线性回归方程预测该奶茶店这种饮料的销量(取整数).
;若气象台预报6月7日白天的平均气温为35℃,根据线性回归方程预测该奶茶店这种饮料的销量(取整数).
附:线性回归方程![]() 中,
中,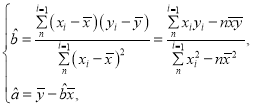 其中
其中![]() ,
,![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() 是椭圆短轴的一个顶点,并且
是椭圆短轴的一个顶点,并且![]() 是面积为
是面积为![]() 的等腰直角三角形.
的等腰直角三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,过
两点,过![]() 作与
作与![]() 轴垂直的直线
轴垂直的直线![]() ,已知点
,已知点![]() ,问直线
,问直线![]() 与
与![]() 的交点的横坐标是否为定值?若是,则求出该定值;若不是,请说明理由.
的交点的横坐标是否为定值?若是,则求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.
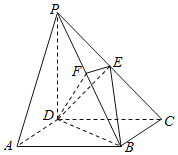
(1)求证:PA∥平面BDE;
(2)求证:PB⊥平面DEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 的最小值是
的最小值是![]() (
(![]() 为坐标原点).
为坐标原点).
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)已知动直线![]() 与圆
与圆![]() :
:![]() 相切,且与椭圆
相切,且与椭圆![]() 交于
交于![]() ,
,![]() 两点.是否存在实数
两点.是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为R,且对于任意x∈R,都有
的定义域为R,且对于任意x∈R,都有![]() 及
及![]() 成立,当
成立,当![]() 且
且![]() 时,都有
时,都有![]() 成立,下列四个结论中不正确命题是( )
成立,下列四个结论中不正确命题是( )
A.![]() B.函数
B.函数![]() 在区间
在区间![]() 上为增函数
上为增函数
C.直线![]() 是函数
是函数![]() 的一条对称轴D.方程
的一条对称轴D.方程![]() 在区间
在区间![]() 上有4个不同的实根
上有4个不同的实根
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1:x2+y2=1与圆C2:x2+y2﹣6x+m=0.
(1)若圆C1与圆C2外切,求实数m的值;
(2)在(1)的条件下,若直线x+2y+n=0与圆C2的相交弦长为2![]() ,求实数n的值.
,求实数n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com