练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．已知等比数列{an}的前n项和为Sn，若$\frac{S_4}{a_4}=\frac{S_2}{a_2}$，则$\frac{{{S_{2015}}}}{S_1}$等于（　　）
    A．2015B．-2015C．1D．-1

    分析 由题意和求和公式可得q的方程，解方程可得q，可得S2015，进而可得比值．

    解答 解：由题意可得等比数列{an}的公比q≠1，
    ∵$\frac{S_4}{a_4}=\frac{S_2}{a_2}$，∴S4a2=S2a4，
    ∴$\frac{{a}_{1}（1-{q}^{4}）}{1-q}$•a1q=$\frac{{a}_{1}（1-{q}^{2}）}{1-q}$•a1q3，
    化简并解方程可得q=-1，
    ∴S2015=$\frac{{a}_{1}[1-（-1）^{2015}]}{1-（-1）}$=a1，
    ∴$\frac{{{S_{2015}}}}{S_1}$=$\frac{{a}_{1}}{{a}_{1}}$=1
    故选：C．

    点评 本题考查等比数列的性质和求和公式，求出数列的公比是解决问题的关键，属基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    2．设函数f（x）=$\frac{1}{{1+px+q{x^2}}}$（其中p2+q2≠0），且存在无穷数列{an}，使得函数在其定义域内还可以表示为f（x）=1+a1x+a2x2+…+anxn+…．
    （1）求a2（用p，q表示）；
    （2）当p=-1，q=-1时，令bn=$\frac{{{a_{n+1}}}}{{{a_n}{a_{n+2}}}}$，设数列{bn}的前n项和为Sn，求证：Sn＜$\frac{3}{2}$；
    （3）若数列{an}是公差不为零的等差数列，求{an}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的中心为O，它的一个顶点为（0，1），离心率为$\frac{{\sqrt{2}}}{2}$，过其右焦点的直线交该椭圆于A，B两点．
    （1）求这个椭圆的方程；
    （2）若OA⊥OB，求△OAB的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．一几何体的三视图如图所示，则该几何体的体积为（　　）
    A．$4-\frac{π}{3}$B．$\frac{8}{3}$C．4-πD．$12-2\sqrt{2}π$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

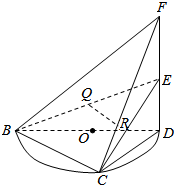    7．如图：$\widehat{BCD}$是直径为$2\sqrt{2}$的半圆，O为圆心，C是$\widehat{BD}$上一点，且$\widehat{BC}=2\widehat{CD}$．DF⊥CD，且DF=2，$BF=2\sqrt{3}$，E为FD的中点，Q为BE的中点，R为FC上一点，且FR=3RC．
    （Ⅰ）求证：面BCE⊥面CDF；
    （Ⅱ）求证：QR∥平面BCD；
    （Ⅲ）求三棱锥F-BCE的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．在△ABC中，内角A、B、C的对边分别为a、b、c，B=$\frac{π}{3}$．
    （1）若b=3，$2sinA=sin（A+\frac{π}{3}）$，求A和a，c；
    （2）若sinAsinC=$\frac{1}{2}$，且△ABC的面积为2$\sqrt{3}$，求b的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．4月23人是“世界读书日”，某中学在此期间开展了一系列的读书教育活动，为了解本校学生课外阅读情况，学校随机抽取了100名学生对其课外阅读时间进行调查，下面是根据调查结果绘制的学生日均课外阅读时间（单位：分钟）的频率分布直方图，若将日均课外阅读时间不低于60分钟的学生称为“读书谜”，低于60分钟的学生称为“非读书谜”

    （1）根据已知条件完成下面2×2的列联表，并据此判断是否有99%的把握认为“读书谜”与性别有关？
    非读书迷读书迷合计
    男15
    女45
    合计
    （2）将频率视为概率，现在从该校大量学生中，用随机抽样的方法每次抽取1人，共抽取3次，记被抽取的3人中的“读书谜”的人数为X，若每次抽取的结果是相互独立的，求X的分布列，期望E（X）和方程D（X）
    附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$n=a+b+c+d
    P（K2≥k0）0.1000.0500.0250.0100.001
    k02.7063.8415.0246.63510.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．设函数f（x）=$\frac{1}{2}$+cosx的所有正的零点从小到大排成的数列为{xn}，则数列{xn}的通项公式为xn=$\left\{\begin{array}{l}{-\frac{4}{3}π+2kπ，}&{n=2k-1，k∈{N}^{*}}\\{-\frac{2}{3}π+2kπ，}&{n=2k，k∈{N}^{*}}\end{array}\right.$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．把函数f（x）=sin（2x+ϕ）$（|ϕ|＜\frac{π}{2}）$的图象向左平移$\frac{π}{6}$个单位，得到函数g（x）的图象，若g（x）的图象关于$（-\frac{π}{3}，0）$对称，则$f（-\frac{π}{2}）$=（　　）
    A．$-\frac{1}{2}$B．$\frac{1}{2}$C．$-\frac{{\sqrt{3}}}{2}$D．$\frac{{\sqrt{3}}}{2}$

    查看答案和解析>>

    同步练习册答案