练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．6颗颜色不同的钻石，可穿成几种钻石圈？

    分析 根据环状排列没有首尾之分，将n个元素围城的环状排列剪开看成n个元素排成一排，即共有Ann种排法．由于n个元素共有n种不同的剪法，则环状排列共有$\frac{{A}_{n}^{n}}{n}$种排法，而钻石圈没有反正，故可以求出答案．

    解答 解：因为由于环状排列没有首尾之分，将n个元素围城的环状排列剪开看成n个元素排成一排，即共有Ann种种排法．由于n个元素共有n种不同的剪法，则环状排列共有有$\frac{{A}_{n}^{n}}{n}$种种排法，而钻石圈没有反正，
    故6颗颜色不同的钻石，可穿成$\frac{{A}_{6}^{6}}{6×2}$=60种不同的钻石圈．

    点评 本题主要考查了环状排列问题，本题的关键是由于6个元素共有6种不同的剪法，钻石圈没有反正，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

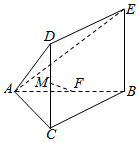    1．在如图所示的空间几何体中，AC⊥BC，四边形DCBE为矩形，点F，M分别为AB，CD的中点．
    （Ⅰ）求证：FM∥平面ADE；
    （Ⅱ）求证：平面ACD⊥平面ADE．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．在△ABC中，角A，B，C的对边分别为a，b，c，已知a2+c2-b2=ac，且$\sqrt{2}$b=$\sqrt{3}$c．
    （1）求角A的大小；
    （2）设函数f（x）=1+cos（2x+B）-cos2x，求函数f（x）的单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．在△ABC中，角A，B，C的对边分别为a，b，c，且acosB-bcosA=c．
    （Ⅰ）求角A；
    （Ⅱ）当△ABC的面积等于4时，求a的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知α是第二象限角，且$sin（{\frac{π}{2}+α}）=-\frac{{\sqrt{5}}}{5}$，则$\frac{{{{cos}^3}α+sinα}}{{cos（{α-\frac{π}{4}}）}}$=（　　）
    A．$-\frac{{11\sqrt{2}}}{15}$B．$-\frac{{9\sqrt{2}}}{5}$C．$\frac{{9\sqrt{2}}}{5}$D．$\frac{{11\sqrt{2}}}{15}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知实数x，y满足x2+y2≤1，则x+y-xy的最大值为1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．多项式（3x+2y）2（x-y）7的展开式中含有x5y4项的系数为-21．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．轴截面为正方形的圆柱，它的全面积与侧面积之比为3：2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．（1+x）+（1+x）2+（1+x）3+（1+x）4+…+（1+x）49展开式中x3的系数是（　　）
    A．${C}_{51}^{3}$B．${C}_{50}^{4}$C．${C}_{51}^{4}$D．${C}_{47}^{4}$

    查看答案和解析>>

    同步练习册答案