
 如图,边长为2的菱形ABCD中,∠A=60°,E、F分别是BC,DC的中点,G为 BF、DE的交点,若$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}$=$\overrightarrow b$
如图,边长为2的菱形ABCD中,∠A=60°,E、F分别是BC,DC的中点,G为 BF、DE的交点,若$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}$=$\overrightarrow b$分析 (1)由题意,根据平面向量的线性表示与运算法则,用$\overrightarrow{AB}$、$\overrightarrow{AD}$表示出$\overrightarrow{AE}$、$\overrightarrow{BF}$与$\overrightarrow{CG}$;
(2)根据平面向量的数量积运算,求出$\overrightarrow{BF}$•$\overrightarrow{CG}$即可.
解答 解:(1)由题意,$\overrightarrow{AE}$=$\overrightarrow{AB}$+$\overrightarrow{BE}$=$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{BC}$=$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$=$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$
$\overrightarrow{BF}$=$\overrightarrow{BC}$+$\overrightarrow{CF}$=$\overrightarrow{AD}$+$\frac{1}{2}$$\overrightarrow{CD}$=$\overrightarrow{AD}$-$\frac{1}{2}$$\overrightarrow{AB}$=$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$,
E、F分别是BC,DC的中点,G为 BF、DE的交点
所以G为△BCD的重心,设BD中点为H,则
$\overrightarrow{CG}$=$\frac{2}{3}$$\overrightarrow{GH}$=$\frac{2}{3}$×$\frac{1}{2}$$\overrightarrow{CA}$=-$\frac{1}{3}$$\overrightarrow{AC}$=-$\frac{1}{3}$($\overrightarrow{a}$+$\overrightarrow{b}$)=-$\frac{1}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$;
(2)$\overrightarrow{BF}•\overrightarrow{CG}=({-\frac{1}{2}\overrightarrow a+\overrightarrow b})•({-\frac{1}{3}\overrightarrow a-\frac{1}{3}\overrightarrow b})$
=$\frac{1}{6}{\overrightarrow a^2}-\frac{1}{6}\overrightarrow a•\overrightarrow b-\frac{1}{3}{\overrightarrow b^2}$
=$\frac{1}{6}$${|\overrightarrow{a}|}^{2}$-$\frac{1}{6}$|$\overrightarrow{a}$||$\overrightarrow{b}$|cos60°-$\frac{1}{3}$${|\overrightarrow{b}|}^{2}$
=$\frac{1}{6}$×4-$\frac{1}{6}$×2×2×$\frac{1}{2}$-$\frac{1}{3}$×4
=-1.
点评 本题考查了平面向量的线性表示与数量积运算问题,是综合性题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 4x | C. | 4+2d | D. | 4+2d2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
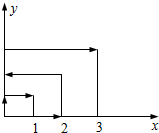 如图:一个质点在第一象限运动,在第一秒钟它由原点运动到点(0,1),而后接着按图所示在与x轴y轴平行的方向运动,且每秒移动一个单位长度,那么416秒后,这个质点所处的位置的坐标是(20,16).
如图:一个质点在第一象限运动,在第一秒钟它由原点运动到点(0,1),而后接着按图所示在与x轴y轴平行的方向运动,且每秒移动一个单位长度,那么416秒后,这个质点所处的位置的坐标是(20,16).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | 6 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com