
���� ����Բ���̵��ص㣬�ɵ�a��0��b��0����a��b����ϳ�ֱ�Ҫ�����Ķ��壬�����жϢ٣�
�����Բ�Ľ���ɵ�˫���ߵ�c���������ʹ�ʽ�ɵ�a����a��b��c�Ĺ�ϵ�ɵ�b�������õ�˫���ߵĽ����߷��̣������жϢڣ�
�������ߵķ��̻�Ϊ�����̣����߷��̣������жϢۣ�
����A��a��0����B��0��b�������������ߵ������ʾ�����a��b����������ľ��빫ʽ�����������ɵ�M�ķ��̣������жϢܣ�
��� �⣺������ax2+by2=1Ϊ��Բ�ɵ�a��0��b��0����a��b��
������ax2+by2=1Ϊ��Բ���ı�Ҫ����������ǡ�a��0��b��0�����ʢٴ���
����˫���ߵ�������e=$\frac{c}{a}$=2��������Բ$\frac{{y}^{2}}{24}$+$\frac{{x}^{2}}{8}$=1����ͬ�Ľ��㣬����c=$\sqrt{24-8}$=4��a=2��b=$\sqrt{16-4}$=2$\sqrt{3}$��
�ɵ�˫���ߵĽ����߷���Ϊy=��$\frac{a}{b}$x��Ϊy=��$\frac{\sqrt{3}}{3}$x���ʢڴ���
��������x=-2y2�ı�����Ϊy2=-$\frac{1}{2}$x���߷���Ϊx=$\frac{1}{8}$���ʢ���ȷ��
�ܳ�Ϊ6���߶�AB�Ķ˵�A��B�ֱ���x��y�����ƶ�������M��x��y������$\overrightarrow{AM}$=2$\overrightarrow{MB}$��
����A��a��0����B��0��b��������x-a=2��-x����y=2��b-y�����ɵ�a=3x��b=$\frac{3}{2}$y����|AB|=6���ɵ�a2+b2=36��
����$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{16}$=1���ʢ���ȷ��
�ʴ�Ϊ���ۢܣ�
���� ���⿼�����������жϣ���Ҫ��Բ���ߵķ��̺����ʣ����齥���߷��̺��߷��̣��Լ��켣���̵���ע�����ô��뷨��ͬʱ�����������ߵ������ʾ�����黯�����������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
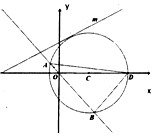 ��ƽ��ֱ������ϵ�У���֪ԲC��x2+y2-4x-1=0��x��������Ľ���ΪD��
��ƽ��ֱ������ϵ�У���֪ԲC��x2+y2-4x-1=0��x��������Ľ���ΪD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com