
分析 (Ⅰ)在△ABC中,利用正弦定理与逆用两角和的正弦可将3acosA=ccosB+bcosC化为3sinAcosA=sinA,从而可求cosA的值;
(Ⅱ)利用二倍角的余弦公式及三角函数间的平方关系可求得cos2A与sin2A的值,再利用两角和的余弦即可求$cos(2A+\frac{π}{3})$的值.
解答 解:(Ⅰ)在△ABC中,由3acosA=ccosB+bcosC,结合正弦定理得:3sinAcosA=sinCcosB+sinBcosC=sin(B+C)=sinA,
因为在△ABC中,sinA≠0,解得cosA=$\frac{1}{3}$,
故cosA的值为$\frac{1}{3}$;--------------------------------6;
(Ⅱ)因为cos2A=2cos2A-1=-$\frac{7}{9}$,A为锐角,
所以,sin2A=$\sqrt{1-{cos}^{2}2A}$=$\frac{4\sqrt{2}}{9}$--------------------------------10;
所以,$cos(2A+\frac{π}{3})$=cos2Acos$\frac{π}{3}$-sin2Asin$\frac{π}{3}$=$\frac{1}{2}$cos2A-$\frac{\sqrt{3}}{2}$sin2A
=-$\frac{7+4\sqrt{6}}{18}$-------------------------------13.
点评 本题考查三角函数的化简求值,突出考查正弦定理的应用,考查等价转化思想与运算求解能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{39}{79}$ | B. | $\frac{1}{80}$ | C. | $\frac{1}{2}$ | D. | $\frac{41}{80}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
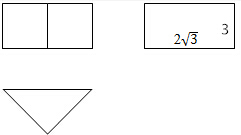 若一个三棱柱ABC-A1B1C1的三视图如图所示,主视图与左视图均为矩形,俯视图为一个正三角形.
若一个三棱柱ABC-A1B1C1的三视图如图所示,主视图与左视图均为矩形,俯视图为一个正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x-1 | B. | y=x-$\frac{1}{2}$ | C. | y=2x-1 | D. | y=$\frac{1}{2}x$-$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
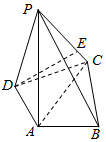 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com