
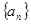 满足
满足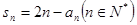 .
.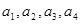 ,并由此猜想通项公式
,并由此猜想通项公式 ;
; 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源:不详 题型:单选题
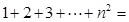
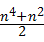 ,则当n=k+1时左端应在n=k的基础上增加 ( )
,则当n=k+1时左端应在n=k的基础上增加 ( ) | A.k2+1 |
| B.(k+1)2 |
C.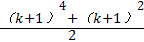 |
| D.(k2+1)+(k2+2)+(k2+3)+…+(k+1)2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
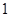 条线段,将圆分割成两部分;画
条线段,将圆分割成两部分;画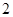 条相交线段,彼此分割成
条相交线段,彼此分割成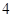 条线段,将圆分割成
条线段,将圆分割成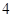 部分;画
部分;画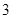 条线段,彼此最多分割成
条线段,彼此最多分割成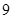 条线段,将圆最多分割成
条线段,将圆最多分割成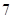 部分;画
部分;画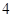 条线段,彼此最多分割成
条线段,彼此最多分割成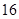 条线段,将圆最多分割成
条线段,将圆最多分割成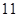 部分.
部分.


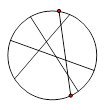
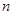 条线段,彼此最多分割成多少条线段?
条线段,彼此最多分割成多少条线段?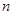 条线段,将圆最多分割成
条线段,将圆最多分割成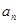 部分,归纳出
部分,归纳出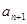 与
与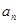 的关系.
的关系.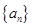 的通项公式,根据
的通项公式,根据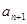 与
与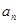 的关系及数列的知识,证明你的猜想是否成立.
的关系及数列的知识,证明你的猜想是否成立.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com