
 在△AOB中,已知∠AOB=$\frac{π}{2}$,∠BAO=$\frac{π}{6}$,AB=4,D为线段AB的中点,△AOC是由△AOB绕直线AO旋转而成,记二面角B-AO-C的大小为θ.
在△AOB中,已知∠AOB=$\frac{π}{2}$,∠BAO=$\frac{π}{6}$,AB=4,D为线段AB的中点,△AOC是由△AOB绕直线AO旋转而成,记二面角B-AO-C的大小为θ.分析 (1)在平面AOB内过B作OD的垂线,垂足为H,证明BH⊥平面COD,可得BH⊥CO,再由OC⊥AO,BH和OA相交,可得OC⊥平面AOB,从而证明OC⊥OB;
(2)在平面BOC中,过O作Ox⊥Oy,以O为原点建立如图所示的空间坐标系,求出平面OCD的一个法向量,由图直接得到平面BOD的一个法向量,然后利用两平面法向量所成角的余弦值求得二面角B-OD-C的余弦值.
解答 解:(1)如图,
在平面AOB内过B作OD的垂线,垂足为H,
∵平面COD⊥平面AOB,平面COD∩平面AOB=OD,
又BH⊥OD,BH⊥平面AOB,
则BH⊥平面COD.
又由OC?平面COD,BH⊥CO,
又∵OC⊥AO,BH和OA相交,
∴OC⊥平面AOB.
又OB?平面AOB,从而OC⊥OB,即θ=$\frac{π}{2}$;
(2)在平面BOC中,过O作Ox⊥Oy,以O为原点建立如图所示的空间坐标系,
则O(0,0,0),D(0,1,2),
∵θ=$\frac{2}{3}$π,求得:C($\sqrt{3}$,-1,0),
设平面OCD的一个法向量为$\overrightarrow{n}=(x,y,z)$,
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{OD}=0}\\{\overrightarrow{n}•\overrightarrow{OC}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{y+2z=0}\\{\sqrt{3}x-y=0}\end{array}\right.$,令x=$\sqrt{3}$,得y=3,z=-$\frac{3}{2}$.
∴$\overrightarrow{n}=(\sqrt{3},3,-\frac{3}{2})$.
又平面OBD的一个法向量为$\overrightarrow{m}=(1,0,0)$,
∴$cos<\overrightarrow{m},\overrightarrow{n}>=\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{\sqrt{3}}{\sqrt{(\sqrt{3})^{2}+{3}^{2}+(-\frac{3}{2})^{2}}×1}=\frac{2\sqrt{171}}{57}$.
∴二面角B-OD-C的余弦值为-$\frac{2\sqrt{171}}{57}$.
点评 本题考查的知识点是与二面角有关的立体几何问题,平面与平面垂直的性质,考查利用空间向量求二面角的平面角,属于中档题.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:解答题
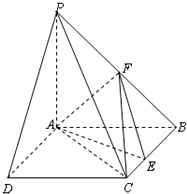 如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动.
如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1,(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,且过点(1,$\frac{{\sqrt{6}}}{3}$).
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1,(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,且过点(1,$\frac{{\sqrt{6}}}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方形ADMN与矩形ABCD所在平面互相垂直,AB=2AD=6.
如图,正方形ADMN与矩形ABCD所在平面互相垂直,AB=2AD=6.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲同学:平均数为2,中位数为2 | B. | 乙同学:中位数为2,唯一的众数为2 | ||
| C. | 丙同学:平均数为2,标准差为2 | D. | 丁同学:平均数为2,唯一的众数为2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其离心率为$\frac{\sqrt{3}}{2}$,两条准线之间的距离为$\frac{8\sqrt{3}}{3}$.B,C分别为椭圆M的上、下顶点,过点T(t,2)(t≠0)的直线TB,TC分别与椭圆M交于E,F两点.
如图,已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其离心率为$\frac{\sqrt{3}}{2}$,两条准线之间的距离为$\frac{8\sqrt{3}}{3}$.B,C分别为椭圆M的上、下顶点,过点T(t,2)(t≠0)的直线TB,TC分别与椭圆M交于E,F两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com