
分析 由题意和平方关系化简已知的式子,由二倍角的正弦公式求出sin2α,由条件和三角函数值的符号缩小α的范围,求出2α的范围,由平方关系和三角函数值的符号求出cos2α.
解答 解:由题意得,sinα+cosα=$\frac{\sqrt{3}}{3}$,
两边平方得,1-2sinαcosα=$\frac{1}{3}$,则sin2α=$\frac{2}{3}$,
因α是第二象限角,sinα+cosα=$\frac{\sqrt{3}}{3}$>0,
所以|sinα|>|cosα|,即$\frac{π}{2}+2kπ<α<\frac{3π}{4}+2kπ(k∈Z)$,
所以$π+4kπ<2α<\frac{3π}{2}+4kπ(k∈Z)$,
则cos2α=-$\sqrt{1-si{n}^{2}2α}$=$-\frac{\sqrt{5}}{3}$,
即sin2α=$\frac{2}{3}$,cos2α=$-\frac{\sqrt{5}}{3}$.
点评 本题考查二倍角的正弦公式,平方关系、三角函数值的符号,以及α范围判断的方法,属于中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
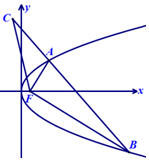 如图,A,B为抛物线y2=4x上的两点,F为抛物线的焦点且FA⊥FB,C为直线AB上一点且横坐标为-1,连结FC.若|BF|=3|AF|,则tanC=$\frac{1}{2}$.
如图,A,B为抛物线y2=4x上的两点,F为抛物线的焦点且FA⊥FB,C为直线AB上一点且横坐标为-1,连结FC.若|BF|=3|AF|,则tanC=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
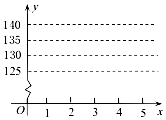 某小卖部为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数y与当天气温(平均温度)x/°C的对比表:
某小卖部为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数y与当天气温(平均温度)x/°C的对比表:| x | 0 | 1 | 3 | 4 |
| y | 140 | 136 | 129 | 125 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com