
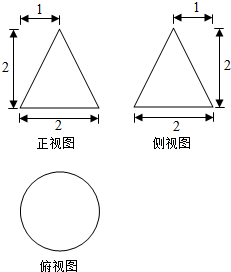
 某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=$\frac{新工件的体积}{原工件的体积}$)( )
某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=$\frac{新工件的体积}{原工件的体积}$)( )| A. | $\frac{8}{9π}$ | B. | $\frac{16}{9π}$ | C. | $\frac{4(\sqrt{2}-1)^{3}}{π}$ | D. | $\frac{12(\sqrt{2}-1)^{3}}{π}$ |
分析 根据三视图可判断其为圆锥,底面半径为1,高为2,求解体积.
利用几何体的性质得出此长方体底面边长为n的正方形,高为x,
利用轴截面的图形可判断得出n=$\sqrt{2}$(1-$\frac{1}{2}x$),0<x<2,求解体积式子,利用导数求解即可,最后利用几何概率求解即.
解答 解:根据三视图可判断其为圆锥,
∵底面半径为1,高为2,
∴V=$\frac{1}{3}×π×{1}^{2}$×2=$\frac{2π}{3}$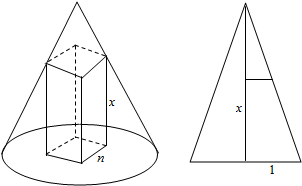
∵加工成一个体积尽可能大的长方体新工件,
∴此长方体底面边长为n的正方形,高为x,
∴根据轴截面图得出:$\frac{x}{2}$=$\frac{1-\frac{\sqrt{2}n}{2}}{1}$,
解得;n=$\sqrt{2}$(1-$\frac{1}{2}x$),0<x<2,
∴长方体的体积Ω=2(1-$\frac{1}{2}x$)2x,Ω′=$\frac{3}{2}$x2-4x+2,
∵,Ω′=$\frac{3}{2}$x2-4x+2=0,x=$\frac{2}{3}$,x=2,
∴可判断(0,$\frac{2}{3}$)单调递增,($\frac{2}{3}$,2)单调递减,
Ω最大值=2(1-$\frac{1}{2}×\frac{2}{3}$)2×$\frac{2}{3}$=$\frac{16}{27}$,
∴原工件材料的利用率为$\frac{\frac{16}{27}}{\frac{2π}{3}}$=$\frac{16}{27}$×$\frac{3}{2π}$=$\frac{8}{9π}$,
故选:A
点评 本题很是新颖,知识点融合的很好,把立体几何,导数,概率都相应的考查了,综合性强,属于难题.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 18 | C. | 25 | D. | $\frac{81}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | a>0,b<0,c>0,d>0 | B. | a>0,b<0,c<0,d>0 | C. | a<0,b<0,c<0,d>0 | D. | a>0,b>0,c>0,d<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数,且在(0,1)上是增函数 | B. | 奇函数,且在(0,1)上是减函数 | ||
| C. | 偶函数,且在(0,1)上是增函数 | D. | 偶函数,且在(0,1)上是减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com