
���� ��1�����ߵļ����귽�̼���2=2��cos�ȣ����ݼ������ֱ������Ļ�����ʽ��x2+y2=2x����������ֱ�����귽�̣�
��2��ֱ��l�ķ��̻�Ϊ��ͨ���̣������и��߶����ɵý��ۣ�
��� �⣺��1���ߦ�=2cos�ȣ����2=2��cos�ȣ���x2+y2=2x��������ֱ�����귽��Ϊ��x-1��2+y2=1��
��2��ֱ��l��$\left\{\begin{array}{l}{x=5+\frac{\sqrt{3}}{2}t}\\{y=\sqrt{3}+\frac{1}{2}t}\end{array}\right.$��tΪ����������ͨ����Ϊ$y=\frac{\sqrt{3}}{3}x-\frac{2\sqrt{3}}{3}$����5��$\sqrt{3}$����ֱ��l�ϣ�
����M��Բ�����ߣ��е�ΪT����|MT|2=��5-1��2+3-1=18��
���и��߶������ɵ�|MT|2=|MA|•|MB|=18��
���� ������Ҫ����Ѽ����귽�̻�Ϊֱ�����귽�̵ķ��������ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | $\frac{6}{7}$ | B�� | $\frac{3}{7}$ | C�� | $\frac{8}{9}$ | D�� | $\frac{4}{9}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
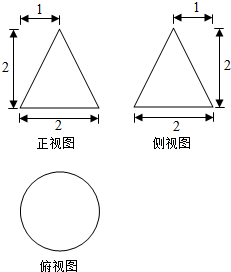 ij����������ͼ��ͼ��ʾ���ֽ��ù���ͨ���������ӹ���һ����������ܴ�ij������¹�������ʹ�¹�����һ��������ԭ������һ�����ڣ���ԭ�������ϵ�������Ϊ������������=$\frac{�¹��������}{ԭ���������}$����������
ij����������ͼ��ͼ��ʾ���ֽ��ù���ͨ���������ӹ���һ����������ܴ�ij������¹�������ʹ�¹�����һ��������ԭ������һ�����ڣ���ԭ�������ϵ�������Ϊ������������=$\frac{�¹��������}{ԭ���������}$����������| A�� | $\frac{8}{9��}$ | B�� | $\frac{16}{9��}$ | C�� | $\frac{4��\sqrt{2}-1��^{3}}{��}$ | D�� | $\frac{12��\sqrt{2}-1��^{3}}{��}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | $\frac{23}{5}$ | C�� | 6 | D�� | $\frac{31}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1440�� | B�� | 1360�� | C�� | 1282�� | D�� | 1128�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com