
分析 (1)直接利用数量积的坐标运算求$\overrightarrow{a}$•$\overrightarrow{b}$;利用向量的坐标加法运算求得$\overrightarrow{a}$+$\overrightarrow{b}$,再利用向量模的公式求模;
(2)①把λ=$\frac{1}{2}$代入f(x),求出cosx的范围后利用换元法求f(x)的最值;
②换元,然后求出二次函数的对称轴方程,再对λ分段求f(x)的最小值g(λ).
解答 解:(1)量$\overrightarrow{a}$=(cos$\frac{3}{2}$x,sin$\frac{3}{2}$x),$\overrightarrow{b}$=(cos$\frac{1}{2}$x,-sin$\frac{1}{2}$x),
则$\overrightarrow{a}$•$\overrightarrow{b}$=cos$\frac{3}{2}$xcos$\frac{1}{2}$x-sin$\frac{3}{2}$xsin$\frac{1}{2}$x=cos($\frac{3}{2}x+\frac{1}{2}x$)=cos2x;
$\overrightarrow{a}+\overrightarrow{b}$=(cos$\frac{3}{2}$x+cos$\frac{1}{2}$x,sin$\frac{3}{2}$x-sin$\frac{1}{2}$x),
$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{(cos\frac{3}{2}x+cos\frac{1}{2}x)^{2}+(sin\frac{3}{2}x-sin\frac{1}{2}x)^{2}}$=$\sqrt{2+2cos2x}=2cosx$(x∈[0,$\frac{π}{2}$]);
(2)f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$-2λ|$\overrightarrow{a}$+$\overrightarrow{b}$|=cos2x-4λcosx.
①当λ=$\frac{1}{2}$时,求f(x)=cos2x-2cosx=2cos2x-2cosx-1,
令t=cosx(x∈[0,$\frac{π}{2}$]),则t∈[0,1],
则y=2t2-2t-1,对称轴方程为t=$\frac{1}{2}$,
当t=$\frac{1}{2}$时,${y}_{min}=2×(\frac{1}{2})^{2}-2×\frac{1}{2}-1=-\frac{3}{2}$;当t=0,t=1时,ymax=-1.
②f(x)=cos2x-4λcosx=2cos2x-4λcosx-1.
令t=cosx(x∈[0,$\frac{π}{2}$]),则t∈[0,1],
则y=2t2-4λt-1.
对称轴方程为t=λ.
当λ≤0时,g(λ)=-1;当λ≥1时,g(λ)=1-4λ;当0<λ<1时,g(λ)=-2λ2-1.
综上,g(λ)=$\left\{\begin{array}{l}{-1,λ≤0}\\{-2{λ}^{2}-1,0<λ<1}\\{1-4λ,λ≥1}\end{array}\right.$.
点评 本题考查了平面向量数量积,考查了向量模的求法,训练了换元法求二次函数的最值,体现了分类讨论的数学思想方法,是中档题.


科目:高中数学 来源: 题型:选择题
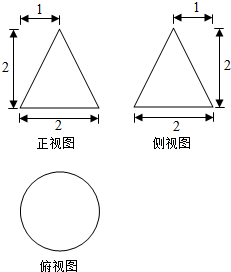 某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=$\frac{新工件的体积}{原工件的体积}$)( )
某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=$\frac{新工件的体积}{原工件的体积}$)( )| A. | $\frac{8}{9π}$ | B. | $\frac{16}{9π}$ | C. | $\frac{4(\sqrt{2}-1)^{3}}{π}$ | D. | $\frac{12(\sqrt{2}-1)^{3}}{π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1440种 | B. | 1360种 | C. | 1282种 | D. | 1128种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 大于8 | C. | $\frac{242}{31}$ | D. | $\frac{240}{41}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 高三年级267位学生参加期末考试,某班37位学生的语文成绩,数学成绩与总成绩在全年级的排名情况如图所示,甲、乙、丙为该班三位学生.
高三年级267位学生参加期末考试,某班37位学生的语文成绩,数学成绩与总成绩在全年级的排名情况如图所示,甲、乙、丙为该班三位学生.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com