考点:异面直线及其所成的角
专题:空间角
分析:过点P作PE⊥A1D1,垂足为E,连结B1E,则PE∥AA1,找到平面角,解Rt△B1PE即可.
解答:

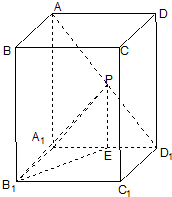
解:(1)解法一:过点P作PE⊥A
1D
1,垂足为E,连结B
1E(如图),则PE∥AA
1,
∴∠B
1PE是异面直线AA
1与B
1P所成的角. (3分)
在 Rt△AA
1D
1中∵∠AD
1A
1=60°,∴∠A
1AD
1=30°,
A1B1=A1D1=AD1=2,
A1E=A1D1=1,
∴
B1E==.又
PE=AA1=.(8分)
∴在 Rt△B
1PE中,
tan∠B1PE===(10分)
∴异面直线AA
1与B
1P所成的角为
arctan. (12分)
解法二:以A
1为原点,A
1B
1所在的直线为x轴建立空间直角坐标
系如图所示,则A
1(0,0,0),
A(0,0,2),B
1(2,0,0),
P(0,1,)(4分)
∴
=(0,0,2),
=(-2,1,)(8分)
∴
cos<,>==
=.(10分)
∴异面直线AA
1与B
1P所成的角为
arccos. (12分)
点评:本题考查了异面直线所成的角的求法,方法一利用将空间角转化为平面角,利用解三角形求之;方法二利用空间向量,建立空间直角坐标系,利用向量的数量积求之.

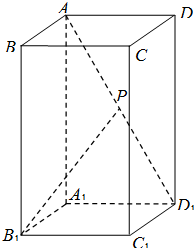 如图,已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,点P是AD1的中点,求异面直线AA1与B1P所成的角(结果用反三角函数表示).
如图,已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,点P是AD1的中点,求异面直线AA1与B1P所成的角(结果用反三角函数表示).
 解:(1)解法一:过点P作PE⊥A1D1,垂足为E,连结B1E(如图),则PE∥AA1,
解:(1)解法一:过点P作PE⊥A1D1,垂足为E,连结B1E(如图),则PE∥AA1,

 名校课堂系列答案
名校课堂系列答案 如图,在底面积边长为1,侧棱长为2的正四棱柱ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.
如图,在底面积边长为1,侧棱长为2的正四棱柱ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.