
| A. | $\frac{3}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 由题意知本题是一个几何概型,试验包含的所有事件是Ω={(x,y)|0≤x≤1,0≤y≤1},写出满足条件的事件是A={(x,y)|0≤x≤1,0≤y≤1,y-x<$\frac{1}{2}$或y<x},算出事件对应的集合表示的面积,根据几何概型概率公式得到结果
解答 解:由题意知本题是一个几何概型,设甲到的时间为x,乙到的时间为y,
则试验包含的所有事件是Ω={(x,y)|0≤x≤1,0≤y≤1},
事件对应的集合表示的面积是s=1,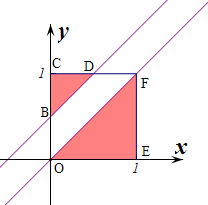
满足条件的事件是A={(x,y)|0≤x≤1,0≤y≤1,y-x<$\frac{1}{2}$或y>x},
则B(0,$\frac{1}{2}$),D($\frac{1}{2}$,1),C(0,1),
则事件A对应的集合表示的面积是1-$\frac{1}{2}$×$\frac{1}{2}$×$\frac{1}{2}$+$\frac{1}{2}$×1×1=$\frac{3}{8}$,根据几何概型概率公式得到P=$\frac{\frac{3}{8}}{1}=\frac{3}{8}$
所以甲、乙两人能见面的概率是1-$\frac{5}{8}=\frac{3}{8}$;
故选A.
点评 本题主要考查几何概型的概率计算,对于这样的问题,一般要通过把试验发生包含的事件所对应的区域求出,根据集合对应的图形面积,用面积的比值得到结果


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -$\frac{2}{3}$ | C. | -$\frac{12}{5}$ | D. | $\frac{\sqrt{2}-4}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{5\sqrt{2}+1}{7}$ | C. | $\frac{1}{3}$ | D. | -$\frac{7}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,10] | B. | [$\sqrt{2}$,$\sqrt{10}$] | C. | (2,10) | D. | [2,10) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
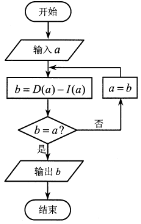 设a是一个各位数字都不是0且没有重复数字的三位数,将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a),(例如a=746,
设a是一个各位数字都不是0且没有重复数字的三位数,将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a),(例如a=746,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com