
| A�� | -4 | B�� | 4 | C�� | 28 | D�� | -10 |
���� ��Լ����������������������DΪ����ֱ�������Σ�������õ�m��ֵ�������������������ʾ�ɵ�Z=2x+4y����Ϊֱ�߷��̵�б��ʽ�����ν�ϵõ����Ž⣬����������������Ž�����꣬����Ŀ�꺯���ô𰸣�
��� �⣺��Լ������$\left\{\begin{array}{l}{x-y��-4}\\{x+y��0}\\{x��m}\end{array}\right.$������������ͼ��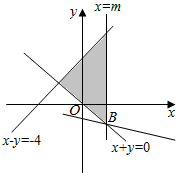
����DΪ����ֱ�������Σ�
�����������Ϊ16�ɵ�m=2��
��Z=$\overrightarrow{OM}$•$\overrightarrow{OA}$=2x+4y��
����$\left\{\begin{array}{l}{x=2}\\{x+y=0}\end{array}\right.$�����B��2��-2����
��Ŀ�꺯��Z=2x+4yΪ$y=-\frac{x}{2}+\frac{Z}{4}$��
��ͼ��֪����ֱ��$y=-\frac{x}{2}+\frac{Z}{4}$����B��2��-2��ʱֱ����y���ϵĽؾ���С��Zȡ��СֵΪ2��2+4����-2��=-4��
��ѡ��A��
���� ���⿼������Թ滮�����������ν�ϵĽ���˼�뷽�������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $\sqrt{2}$ | C�� | 2$\sqrt{2}$ | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2015 | D�� | 2016 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [0��2�� | B�� | ��-2��0] | C�� | [0��+�ޣ� | D�� | ��-�ޣ�0] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com