
分析 根据${∫}_{0}^{1}$f(x)dx是常数,得出f(x)是一次函数,利用待定系数法即可求出f(x)的解析式.
解答 解:∵f(x)为连续函数,且f(x)=x-2${∫}_{0}^{1}$f(x)dx,
不妨设2${∫}_{0}^{1}$f(x)dx=b(b为常数),
∴f(x)=x-b,
∴f(x)=x-2${∫}_{0}^{1}$f(x)dx=x-2${∫}_{0}^{1}$(x-b)dx
=x-2$(\frac{1}{2}{x}^{2}-bx){|}_{0}^{1}$=x-1+2b,
∴-b=-1+2b,解得b=$\frac{1}{3}$,
∴f(x)=x-$\frac{1}{3}$.
点评 本题考查了利用待定系数法求函数解析式的应用问题,考查了定积分简单应用,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {y|y=x2-1} | B. | {y|y=2x} | C. | {y|y=lgx} | D. | {y|y=x2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
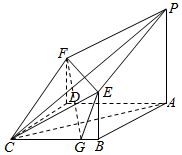 如图所示的几何体由平面PECF截棱长为2的正方体得到,其中P、C为原正方体的顶点,E、F为原正方体侧棱的中点,正方形ABCD为原正方体的底面,点G为线段BC上的动点.
如图所示的几何体由平面PECF截棱长为2的正方体得到,其中P、C为原正方体的顶点,E、F为原正方体侧棱的中点,正方形ABCD为原正方体的底面,点G为线段BC上的动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com