
【题目】设向量a=(sinx-1,1),b=(sinx+3,1),c=(-1,-2),d=(k,1),k∈R.
(1)若x∈[-![]() ,
,![]() ],且a∥(b+c),求x的值;
],且a∥(b+c),求x的值;
(2)若存在x∈R,使得(a+d)⊥(b+c),求k的取值范围.
【答案】(1) x=-![]() . (2) k的取值范围是[
. (2) k的取值范围是[![]() ,4].
,4].
【解析】
试题分析:(1)运用向量的共线的坐标表示及三角函数的图象和性质,即可解得![]() ;
;
(2)运用向量的垂直的条件,以及参数分离和正弦函数的值域,即可求得![]() 的范围.
的范围.
试题解析:(1)由于b=(sinx+3,1),c=(-1,-2),则b+c=(sinx+2,-1)
a=(sinx-1,1),且a∥(b+c),则有sinx+2=1-sinx,即sinx=-![]() ,
,
由于x∈[-![]() ,
,![]() ],则x=-
],则x=-![]() .
.
(2)若存在x∈R,使得(a+d)⊥(b+c),则有(sinx-1+k,2)(sinx+2,-1)=0,
即有k=![]() +1-sinx,令2+sinx=t(1≤t≤3)
+1-sinx,令2+sinx=t(1≤t≤3)
则k=![]() -t+3,k′=-
-t+3,k′=-![]() -1<0,则k在[1,3]上递减,
-1<0,则k在[1,3]上递减,
则有![]() ≤k≤4,故k的取值范围是[
≤k≤4,故k的取值范围是[![]() ,4].
,4].


科目:高中数学 来源: 题型:
【题目】设双曲线![]() 的左,右焦点分别为F1,F2,过F1的直线l交双曲线左支于A,B两点,则|BF2|+|AF2|的最小值为( )
的左,右焦点分别为F1,F2,过F1的直线l交双曲线左支于A,B两点,则|BF2|+|AF2|的最小值为( )
A. ![]() B. 11
B. 11
C. 12 D. 16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,则( )
A.△A1B1C1和△A2B2C2都是锐角三角形
B.△A1B1C1和△A2B2C2都是钝角三角形
C.△A1B1C1是钝角三角形,△A2B2C2是锐角三角形
D.△A1B1C1是锐角三角形,△A2B2C2是钝角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型高端制造公司为响应《中国制造2025》中提出的坚持“创新驱动、质量为先、绿色发展、结构优化、人才为本”的基本方针,准备加大产品研发投资,下表是该公司2017年5~12月份研发费用(百万元)和产品销量(万台)的具体数据:

(1)根据数据可知![]() 与
与![]() 之间存在线性相关关系
之间存在线性相关关系
(i)求出![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() );
);
(ii)若2018年6月份研发投人为25百万元,根据所求的线性回归方程估计当月产品的销量;
(2)公司在2017年年终总结时准备从该年8~12月份这5个月中抽取3个月的数据进行重点分析,求没有抽到9月份数据的概率.
参考数据: ![]() ,
,![]() .
.
参考公式:对于一组数据![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: 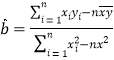 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是角A、B、C的对边,x=(2a+c,b),y=(cosB,cosC),且x·y=0.
(1)求B的大小;
(2)若b=![]() ,求|
,求|![]() |的最小值.
|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集为R,函数f(x)=lg(1﹣x)的定义域为集合A,集合B={x|x2﹣x﹣6>0}.
(Ⅰ)求A∪B;
(Ⅱ)若C={x|m﹣1<x<m+1},C(A∩(RB)),求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知从![]() 地去
地去![]() 地有①或②两条路可走,并且汽车走路①堵车的概率为
地有①或②两条路可走,并且汽车走路①堵车的概率为![]() ,汽车走路②堵车的概率为
,汽车走路②堵车的概率为![]() ,若现在有两辆汽车走路①,有一辆汽车走路②,且这三辆车是否堵车相互之间没有影响,
,若现在有两辆汽车走路①,有一辆汽车走路②,且这三辆车是否堵车相互之间没有影响,
(1)若这三辆汽车中恰有一辆汽车被堵的概率为![]() ,求走路②堵车的概率;
,求走路②堵车的概率;
(2)在(1)的条件下,求这三辆汽车中被堵车辆的辆数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com