
分析 设两串彩灯第一次闪亮的时刻分别为x,y,由题意可得0≤x≤4,0≤y≤4,要满足条件须|x-y|≤2,作出其对应的平面区域,由几何概型可得答案.
解答  解:设这两只玩具狗第一次闪亮的时刻分别为x,y
解:设这两只玩具狗第一次闪亮的时刻分别为x,y
由已知:$\left\{\begin{array}{l}0≤x≤4\\ 0≤y≤4\end{array}\right.$
由第一次闪亮时刻相差不超过两秒可得|x-y|≤2…(6分)
现记“这两只玩具狗第一次闪亮的时刻不超过2秒”为事件A.
则$P(A)=1-\frac{{2×\frac{1}{2}×{2^2}}}{4^2}=1-\frac{1}{4}=\frac{3}{4}$…(11分)
答:这两只玩具狗第一次闪亮的时刻不超过2秒的概率为$\frac{3}{4}$.…(12分)
点评 本题考查几何概型,涉及用一元二次方程组表示平面区域,属基础题.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
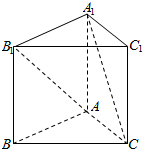 如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,则异面直线AB1和A1C所成的角的余弦值大小为( )
如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,则异面直线AB1和A1C所成的角的余弦值大小为( )| A. | $\frac{1}{4}$ | B. | $-\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
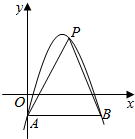 姐图,在平面直角坐标系中,抛物线y=-(x-2)2+3与y轴交于点A,过点A与x轴平行的直线交抛物线于另一点B,点P是直线AB上方的抛物线上一点,设点P的横坐标为m,则△PAB的面积S的取值范围为0<S≤8.
姐图,在平面直角坐标系中,抛物线y=-(x-2)2+3与y轴交于点A,过点A与x轴平行的直线交抛物线于另一点B,点P是直线AB上方的抛物线上一点,设点P的横坐标为m,则△PAB的面积S的取值范围为0<S≤8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com