
| A. | [0,1] | B. | [0,1) | C. | [0,+∞) | D. | [1,+∞) |
分析 根据新定义a*b=$\left\{\begin{array}{l}{a,(a≤b)}\\{b,(a>b)}\end{array}\right.$,求解2x*2-x的值域即可.
解答 解:根据新定义a*b=$\left\{\begin{array}{l}{a,(a≤b)}\\{b,(a>b)}\end{array}\right.$,
那么:2x*2-x=$\left\{\begin{array}{l}{{2}^{x},({2}^{x}≤{2}^{-x})}\\{{2}^{-x},({2}^{x}>{2}^{-x})}\end{array}\right.$,
∴函数f(x)=|2x*2-x-1|=$\left\{\begin{array}{l}{|{2}^{x}-1|,x≤0}\\{|{2}^{-x}-1|,x>0}\end{array}\right.$,
又∵当x≤0时,2x∈(0,1],
∴-1<2x-1≤0,
则:|2x-1|∈[0,1),
又∵当x>0时,2-x∈(0,1),
∴-1<2-x-1<0,
则:|2-x-1|∈(0,1),
综上所得函数f(x)=|2x*2-x-1|的值域为[0,1).
故选:B.
点评 本题考查了新定义的理解,读懂题意非常关键.同时考查了分段函数的定义域和值域的求法.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}$ | B. | $\frac{16}{3}$ | C. | 8 | D. | $\frac{8\sqrt{5}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 10 | C. | $\frac{5}{2}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{8}$ | C. | $\frac{3}{2}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
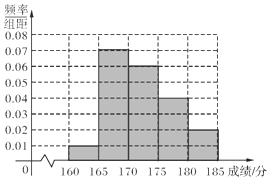 某校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,被抽取学生的成绩均不低于160分,且低于185分,如图是按成绩分组得到的频率分布直方图.
某校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,被抽取学生的成绩均不低于160分,且低于185分,如图是按成绩分组得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com