
分析 结合双曲线的性质$\frac{b}{a}$=$\sqrt{3}$,0=$\sqrt{3}$c-4$\sqrt{3}$,求出a,c即可.
解答 解:过双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的渐近线方程为y=±$\frac{b}{a}$x,
因为过双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点F的直线l:y=$\sqrt{3}x-4\sqrt{3}$与C只有一个公共点,
所以$\frac{b}{a}$=$\sqrt{3}$,0=$\sqrt{3}$c-4$\sqrt{3}$,
又因为a2+b2=c2,
解得c=3,a=$\frac{3}{2}$,
所以2c=8,e=$\frac{c}{a}$=2,
故答案为:8,2
点评 本题给出双曲线方程,求经过双曲线的右交点且与双曲线只有一个公共点的直线的条数.着重考查了直线的方程、双曲线的标准方程与简单几何性质等知识,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
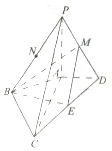 在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N,E分别为PD,PB,CD的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N,E分别为PD,PB,CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{π}{3}$ | B. | -$\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2倍以上,但不超过3倍 | B. | 3倍以上,但不超过4倍 | ||
| C. | 4倍以上,但不超过5倍 | D. | 5倍以上,但不超过6倍 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6π | B. | ($\sqrt{2}$+$\sqrt{5}$+1)π | C. | (2$\sqrt{2}$+2$\sqrt{5}$)π | D. | ($\sqrt{2}$+$\sqrt{5}$)π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com