考点:数列与函数的综合
专题:等差数列与等比数列
分析:由数列的求和和分段函数,得到S104-S96=a97+a98+a99+a100+a101+a102+a103+a104=f(97)+f(98)+f(99)+f(100)+f(101)+f(102)+f(103)+f(104),
再运用诱导公式求出三角函数值,从而得到答案.
解答:
解:∵S
104=a
1+a
2+a
3+…+a
104,S
96=a
1+a
2+a
3+…+a
96,
∴S
104-S
96=a
97+a
98+a
99+a
100+a
101+a
102+a
103+a
104=f(97)+f(98)+f(99)+f(100)+f(101)+f(102)+f(103)+f(104)
=[-sin(
)+2×48+2]+[-sin(
)+2×49]+[sin(
)+2×49+2]+[sin
+2×50]+[-sin
+2×50+2]+[-sin
+2×51]
+[sin
+2×51+2]+[sin
+2×52]
=97+98+99+100+101+102+103+104
=
=804.
故答案为:804.
点评:本题考查分段函数及应用,考查数列的求和,三角函数的求值,考查基本的运算能力,属于中档题.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案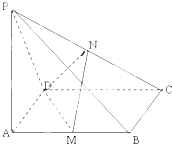 如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AD,M,N分别是AB,PC的中点.
如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AD,M,N分别是AB,PC的中点.