Question

17．已知二面角α-l-β为锐角，A∈a，A到平面β的距离AH=2$\sqrt{3}$，点A到棱的距离为AB=4，则二面角α-l-β的大小为（　　）

• A． 15°
• B． 50°
• C． 60°
• D． 45°

Answer 1

分析 连接BH，便可说明∠ABH为二面角α-l-β的平面角，从而在Rt△ABH中可求出sin∠ABH，从而求得∠ABH．

解答 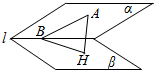解：如图，连接BH；
AH⊥β，l?β；
∴AH⊥l，又AB⊥l，AB∩AH=A；
∴l⊥平面ABH；
∴l⊥BH；
∴∠ABH为二面角α-l-β的平面角；
在Rt△ABH中，AH=$2\sqrt{3}$，AB=4，∠AHB=90°，∴$sin∠ABH=\frac{AH}{AB}=\frac{\sqrt{3}}{2}$；
∴∠ABH=60°．
故选：C．

点评 考查平面上一点到另一平面距离的概念，空间一点到一直线的距离的概念，线面垂直的性质，线面垂直的判定定理，以及二面角的平面角的定义及求法，本题是将二面角平面角放在直角三角形中求解．