
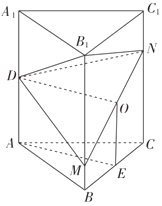
【题目】如图,三棱柱ABC﹣A1B1C1各条棱长均为4,且AA1⊥平面ABC,D为AA1的中点,M,N分别在线段BB1和线段CC1上,且B1M=3BM,CN=3C1N,

(1)证明:平面DMN⊥平面BB1C1C;
(2)求三棱锥B1﹣DMN的体积.
【答案】(1)证明见解析 (2)4![]() .
.
【解析】
(1)取线段MN的中点O,线段BC的中点E,可证DO∥AE,以及DO⊥平面BB1C1C,即可证得结论;
(2)用等体积法转化为以D顶点,即可求出体积.
(1)证明:取线段MN的中点O,线段BC的中点E,连接DO,AE,OE,
由题意可得,OE![]() (MB+CN)
(MB+CN)![]() CC1.
CC1.
因为D为AA1的中点,所以AD![]() AA1,
AA1,
因为AA1∥CC1,AA1=CC1,
所以AD∥OE,AD=OE,
所以四边形AEOD为平行四边形,所以DO∥AE.
因为点E为BC的中点,所以AE⊥BC,
因为AA1⊥平面ABC,所以AA1⊥AE,则AE⊥CC1,因为BC∩CC1=C,
所以AE⊥平面BB1C1C,则DO⊥平面BB1C1C,
因为DO平面DMN,所以平面DMN⊥平面BB1C1C.
(2)解:因为B1M=3BM,BB1=4,所以B1M=3.
所以△B1MN的面积S![]() 6.
6.
由(1)可得,DO=AE![]() 2
2![]() .
.
故三棱锥B1﹣DMN的体积为:
V![]() V
V![]() 4
4![]() .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
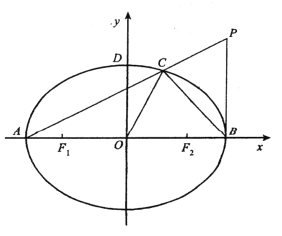
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 分别为左,右焦点,
分别为左,右焦点,![]() 分别为左,右顶点,原点
分别为左,右顶点,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .设点
.设点![]() 在第一象限,且
在第一象限,且![]() 轴,连接
轴,连接![]() 交椭圆于点
交椭圆于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若三角形![]() 的面积等于四边形
的面积等于四边形![]() 的面积,求直线
的面积,求直线![]() 的方程;
的方程;
(3)求过点![]() 的圆方程(结果用
的圆方程(结果用![]() 表示).
表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下命题:
① 双曲线![]() 的渐近线方程为
的渐近线方程为![]() ;
;
② 命题![]() “
“![]() ,
,![]() ”是真命题;
”是真命题;
③ 已知线性回归方程为![]() ,当变量
,当变量![]() 增加
增加![]() 个单位,其预报值平均增加
个单位,其预报值平均增加![]() 个单位;
个单位;
④ 设随机变量![]() 服从正态分布
服从正态分布![]() ,若
,若![]() ,则
,则![]() ;
;
⑤ 已知![]() ,
,![]() ,
,![]() ,
,![]() ,依照以上各式的规律,得到一般性的等式为
,依照以上各式的规律,得到一般性的等式为![]() ,(
,(![]() )
)
则正确命题的序号为 (写出所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
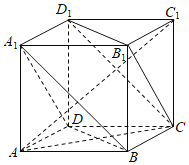
【题目】如图,多面体ABCD﹣A1B1C1D1为正方体,则下面结论正确的是( )
A.A1B∥B1C
B.平面CB1D1⊥平面A1B1C1D1
C.平面CB1D1∥平面A1BD
D.异面直线AD与CB1所成的角为30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线, ![]() ,
,![]() ,
,![]() 是三个不同的平面.有下列四个命题:
是三个不同的平面.有下列四个命题:
①若![]() ,
,![]() ,
,![]() ,则
,则![]() ; ②若
; ②若![]() ,
,![]() ,则
,则![]() ;
;
③ 若![]() ,
,![]() ,
,![]() ,则
,则![]() ;④ 若
;④ 若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
其中错误命题的序号是
A. ①③ B. ①④ C. ②③④ D. ②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司欲生产一款迎春工艺品回馈消费者,工艺品的平面设计如图所示,该工艺品由直角![]() 和以
和以![]() 为直径的半圆拼接而成,点
为直径的半圆拼接而成,点![]() 为半圈上一点(异于
为半圈上一点(异于![]() ,
,![]() ),点
),点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .已知
.已知![]() ,
,![]() ,设
,设![]() .
.

(1)为了使工艺礼品达到最佳观赏效果,需满足![]() ,且
,且![]() 达到最大.当
达到最大.当![]() 为何值时,工艺礼品达到最佳观赏效果;
为何值时,工艺礼品达到最佳观赏效果;
(2)为了工艺礼品达到最佳稳定性便于收藏,需满足![]() ,且
,且![]() 达到最大.当
达到最大.当![]() 为何值时,
为何值时,![]() 取得最大值,并求该最大值.
取得最大值,并求该最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com