
【题目】已知数列{an}满足a1=1,an+1=3an+4,n∈N*.
(1)证明:数列{an+2}是等比数列,并求数列{an}的通项公式;
(2)设bn=(a2n+2)log3(an+2),求数列{bn}的前n项和Tn.
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】某企业开发一种新产品,现准备投入适当的广告费对产品进行促销,在一年内,预计年销量![]() (万件)与广告费
(万件)与广告费![]() (万元)之间的函数关系为
(万元)之间的函数关系为![]() ,已知生产此产品的年固定投入为
,已知生产此产品的年固定投入为![]() 万元,每生产
万元,每生产![]() 万件此产品仍需要投入
万件此产品仍需要投入![]() 万元,若年销售额为“年生产成本的
万元,若年销售额为“年生产成本的![]() ”与“年广告费的
”与“年广告费的![]() ”之和,而当年产销量相等:
”之和,而当年产销量相等:
(1)试将年利润![]() (万元)表示为年广告费
(万元)表示为年广告费![]() (万元)的函数;
(万元)的函数;
(2)求当年广告费投入多少万元时,企业利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有员工1000名,平均每人每年创造利润10万元.为增加企业竞争力,决定优化产业结构,调整出![]() 名员工从事第三产业,调整后平均每人每年创造利润为
名员工从事第三产业,调整后平均每人每年创造利润为![]() 万元
万元![]() ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高![]() .
.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润条件下,若要求调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则![]() 的取值范围是多少?
的取值范围是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差d≠0,且a1,a3,a13成等比数列,若a1=1,Sn为数列{an}的前n项和,则![]() 的最小值为( )
的最小值为( )
A.4B.3C.![]() D.2
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应党中央“扶贫攻坚”的号召,某单位指导一贫困村通过种植紫甘薯来提高经济收入.紫甘薯对环境温度要求较高,根据以往的经验,随着温度的升高,其死亡株数成增长的趋势.下表给出了2017年种植的一批试验紫甘薯在温度升高时6组死亡的株数:

经计算: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() 分别为试验数据中的温度和死亡株数,
分别为试验数据中的温度和死亡株数, ![]() .
.
(1)若用线性回归模型,求![]() 关于
关于![]() 的回归方程
的回归方程![]() (结果精确到
(结果精确到![]() );
);
(2)若用非线性回归模型求得![]() 关于
关于![]() 的回归方程为
的回归方程为![]() ,且相关指数为
,且相关指数为![]() .
.
(i)试与(1)中的回归模型相比,用![]() 说明哪种模型的拟合效果更好;
说明哪种模型的拟合效果更好;
(ii)用拟合效果好的模型预测温度为![]() 时该批紫甘薯死亡株数(结果取整数).
时该批紫甘薯死亡株数(结果取整数).
附:对于一组数据![]() ,
, ![]() ,……,
,……, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:  ;相关指数为:
;相关指数为:  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为菱形,且∠ABC=60°,
中,底面ABCD为菱形,且∠ABC=60°,![]() 平面ABCD,
平面ABCD,![]() ,点E,F为PC,PA的中点.
,点E,F为PC,PA的中点.
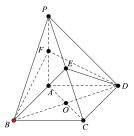
(1)求证:平面BDE⊥平面ABCD;
(2)二面角E—BD—F的大小;
(3)设点M在PB(端点除外)上,试判断CM与平面BDF是否平行,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】郑州一中社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图:将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
(1)根据已知条件完成下面的2×2列联表,并据此资料你是否认为“围棋迷”与性别有关?

非围棋迷 | 围棋迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(2)将上述调查所得到的频率视为概率.现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记被抽取的3名学生中的“围棋迷”人数为![]() .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求![]() 的分布列,期望
的分布列,期望
附:![]() ,
,
| 0.05 | 0.01 |
| 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com