
【题目】已知向量![]() 垂直于向量
垂直于向量![]() ,向量
,向量![]() 垂直于向量
垂直于向量![]() .
.
(1)求向量![]() 与
与![]() 的夹角;
的夹角;
(2)设![]() ,且向量
,且向量![]() 满足
满足![]() ,求
,求![]() 的最小值;
的最小值;
(3)在(2)的条件下,随机选取一个向量![]() ,求
,求![]() 的概率.
的概率.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据向量的垂直,转化出方程组,求解方程组即可;
(2)将向量赋予坐标,求得向量对应点的轨迹方程,将问题转化为圆外一点,到圆上一点的距离的最值问题,即可求解;
(3)根据余弦定理,解得![]() ,以及
,以及![]() 的临界状态时,对应的圆心角的大小,利用几何概型的概率计算公式,即可求解.
的临界状态时,对应的圆心角的大小,利用几何概型的概率计算公式,即可求解.
(1)因为![]()
故可得![]() ,
,![]()
解得![]() ①
①
![]() ②
②
由①-②可得
![]() ,解得
,解得![]() ,
,
将其代入①可得![]() ,即
,即![]()
将其代入②可得![]()
解得![]() ,又向量夹角的范围为
,又向量夹角的范围为![]() ,
,
故向量![]() 与
与![]() 的夹角为
的夹角为![]() .
.
(2)不妨设![]() ,
,![]()
由![]()
可得![]() .
.
不妨设![]() 的起始点为坐标原点,终点为C.
的起始点为坐标原点,终点为C.
因此,点C落在以![]() )为圆心,1为半径的圆上(如图).
)为圆心,1为半径的圆上(如图).

因为![]() ,即
,即![]()
由圆的特点可知![]() 的最小值为
的最小值为![]() ,
,
即:![]() .
.
(3)当![]() 时,因为
时,因为![]() ,
,![]() ,满足勾股定理,
,满足勾股定理,
故容易得![]() .
.
当![]() 时,假设此时
时,假设此时![]() 点落在如图所示的F点处.如图所示.
点落在如图所示的F点处.如图所示.
因为![]() ,由余弦定理容易得
,由余弦定理容易得
![]() ,故
,故![]() .
.

所以,本题化为,在半圆上任取一点C,点C落在弧CF上的概率.
由几何概型的概率计算可知:
![]() 的概率即为圆心角
的概率即为圆心角![]() 的弧度除以
的弧度除以![]() ,
,
即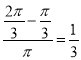 .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 是
是![]() 上的偶函数,对于任意
上的偶函数,对于任意![]() 都有
都有![]() 成立,当
成立,当![]() ,且
,且![]() 时,都有
时,都有![]() .给出以下三个命题:
.给出以下三个命题:
①直线![]() 是函数
是函数![]() 图像的一条对称轴;
图像的一条对称轴;
②函数![]() 在区间
在区间![]() 上为增函数;
上为增函数;
③函数![]() 在区间
在区间![]() 上有五个零点.
上有五个零点.
问:以上命题中正确的个数有( ).
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分别直方图.
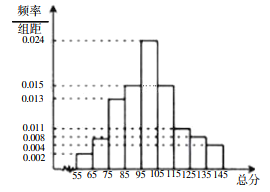
(1)求这100份数学试卷成绩的中位数;
(2)从总分在![]() 和
和![]() 的试卷中随机抽取2份试卷,求抽取的2份试卷中至少有一份总分少于65分的概率.
的试卷中随机抽取2份试卷,求抽取的2份试卷中至少有一份总分少于65分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l经过直线2x+y-5=0与x-2y=0的交点P.
(1)若直线l平行于直线l1:4x-y+1=0,求l的方程;
(2)若直线l垂直于直线l1:4x-y+1=0,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线方程为![]() .
.
(1)证明:直线恒过定点;
(2)![]() 为何值时,点
为何值时,点![]() 到直线的距离最大,最大值为多少?
到直线的距离最大,最大值为多少?
(3)若直线分别与![]() 轴,
轴,![]() 轴的负半轴交于
轴的负半轴交于![]() 两点,求
两点,求![]() 面积的最小值及此时直线的方程.
面积的最小值及此时直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将各项均为整数的数列![]() 排成如图所示的三角形数阵(第
排成如图所示的三角形数阵(第![]() 行有
行有![]() 个数,同一行中,下标小的数排在左边).
个数,同一行中,下标小的数排在左边).![]() 表示数阵中第
表示数阵中第![]() 行第1列的数.
行第1列的数.
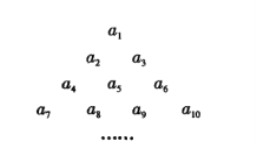
已知数列![]() 为等比数列,且从第3行开始,各行均构成公差为
为等比数列,且从第3行开始,各行均构成公差为![]() 的等差数列,
的等差数列,![]() ,
,![]() ,
,![]() .
.
(1)求数阵中第![]() 行 第
行 第![]() 列的数
列的数 ![]() (用
(用 ![]() 、
、![]() 表示);
表示);
(2)求![]() 的值;
的值;
(3)2013是否在该数阵中,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,为了测量某一隧道两侧A、B两地间的距离,某同学首先选定了不在直线AB上的一点C(![]() 中∠A、∠B、∠C所对的边分别为a、b、c),然后确定测量方案并测出相关数据,进行计算.现给出如下四种测量方案;①测量∠A,∠C,b;②测量∠A,∠B,∠C;③测量a,b,∠C;④测量∠A,∠B,a,则一定能确定A、B间距离的所有方案的序号为( )
中∠A、∠B、∠C所对的边分别为a、b、c),然后确定测量方案并测出相关数据,进行计算.现给出如下四种测量方案;①测量∠A,∠C,b;②测量∠A,∠B,∠C;③测量a,b,∠C;④测量∠A,∠B,a,则一定能确定A、B间距离的所有方案的序号为( )
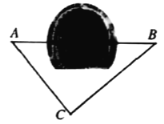
A.①③B.①③④C.②③④D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某儿童乐园在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:
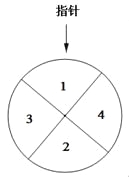
①若![]() ,则奖励玩具一个;
,则奖励玩具一个;
②若![]() ,则奖励水杯一个;
,则奖励水杯一个;
③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.
(Ⅰ)求小亮获得玩具的概率;
(Ⅱ)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com