
【题目】已知数列![]() 满足a1=m,an+1=
满足a1=m,an+1=![]() (k∈N*,r∈R),其前n项和为
(k∈N*,r∈R),其前n项和为![]() .
.
(1)当m与r满足什么关系时,对任意的n∈N*,数列{an}都满足an+2=an?
(2)对任意实数m,r,是否存在实数p与q,使得{a2n+1+p}与{a2n+q}是同一个等比数列.若存在,请求出p,q满足的条件;若不存在,请说明理由;
(3)当m=r=1时,若对任意的n∈N*,都有Sn≥λan,求实数λ的最大值.
【答案】(1)m+r=0;(2)见解析;(3)1.
【解析】试题分析:(1)由a3=a1,得m+r=0,再证m+r=0满足题意即可;
(2)依题意,a2n+1=a2n+r=2a2n-1+r,则a2n+1+r=2(a2n-1+r),当m+r≠0时,{a2n+1+r}是等比数列,由题意可得p=r,q=2r,若m+r=0,则不存在实数p,q,使得{a2n+1+p}与{a2n+q}是等比数列;
(3)当m=r=1时,由(2)可得a2n-1=2n-1,a2n=2n+1-2,由分组求和得
试题解析:
(1)由题意得a1=m,a2=2a1=2m,a3=a2+r=2m+r,
由a3=a1,得m+r=0.
当m+r=0时,因为an+1=![]() (k∈N*),
(k∈N*),
所以a1=a3=…=m,a2=a4=…=2m,故对任意的n∈N*,数列{an}都满足an+2=an. 当n=2k时,Sn=3(2k+1-k-2),再由![]() 的单调性求最小值即可得λ≤
的单调性求最小值即可得λ≤![]() ,当n=2k-1时,Sn=S2k-a2k=2k+2-3k-4,再由
,当n=2k-1时,Sn=S2k-a2k=2k+2-3k-4,再由![]() 的单调性求最小值即可得λ≤
的单调性求最小值即可得λ≤![]() ,从而得解.
,从而得解.
即当实数m,r满足m+r=0时,符合题意.
(2)存在.依题意,a2n+1=a2n+r=2a2n-1+r,
则a2n+1+r=2(a2n-1+r),
因为a1+r=m+r,
所以当m+r≠0时,{a2n+1+r}是等比数列,且a2n+1+r=(a1+r)2n=(m+r)2n.
为使{a2n+1+p}是等比数列,则p=r.
同理,当m+r≠0时,a2n+2r=(m+r)2n,{a2n+2r}是等比数列,欲使{a2n+q}是等比数列,则q=2r.
综上所述,
①若m+r=0,则不存在实数p,q,使得{a2n+1+p}与{a2n+q}是等比数列;
②若m+r≠0,则当p,q满足q=2p=2r时,{a2n+1+p}与{a2n+q}是同一个等比数列.
(3)当m=r=1时,由(2)可得a2n-1=2n-1,a2n=2n+1-2,
当n=2k时,an=a2k=2k+1-2,
Sn=S2k=(21+22+…+2k)+(22+23+…+2k+1)-3k
=3(2k+1-k-2),所以![]() =3
=3![]() .
.
令ck=![]() ,
,
则ck+1-ck=![]() -
-![]() =
=![]() <0,
<0,
所以![]() ≥
≥![]() ,即λ≤
,即λ≤![]() .
.
当n=2k-1时,an=a2k-1=2k-1,
Sn=S2k-a2k=3(2k+1-k-2)-(2k+1-2)=2k+2-3k-4,
所以![]() =4-
=4-![]() ,同理可得
,同理可得![]() ≥1,即λ≤1.
≥1,即λ≤1.
综上所述,实数λ的最大值为1.


科目:高中数学 来源: 题型:
【题目】为缓减人口老年化带来的问题,中国政府在2016年1月1日作出全国统一实施全面的“二孩”政策,生“二孩”是目前中国比较流行的元素![]() 某调查机构对某校学生做了一个是否同意父母生“二孩”抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”
某调查机构对某校学生做了一个是否同意父母生“二孩”抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”![]() 现已得知100人中同意父母生“二孩”占
现已得知100人中同意父母生“二孩”占![]() ,统计情况如表:
,统计情况如表:
性别属性 | 同意父母生“二孩” | 反对父母生“二孩” | 合计 |
男生 | 10 | ||
女生 | 30 | ||
合计 | 100 |
![]() 请补充完整上述列联表;
请补充完整上述列联表;
![]() 根据以上资料你是否有
根据以上资料你是否有![]() 把握,认为是否同意父母生“二孩”与性别有关?请说明理由.
把握,认为是否同意父母生“二孩”与性别有关?请说明理由.
参考公式与数据:![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是首项为a,公差为d的等差数列(d≠0),
是首项为a,公差为d的等差数列(d≠0), ![]() 是其前n项的和.记
是其前n项的和.记![]() ,n∈N*,其中c为实数.
,n∈N*,其中c为实数.
(1)若c=0,且b1,b2,b4成等比数列,证明:Snk=n2Sk(k,n∈N*);
(2)若{![]() }是等差数列,证明:c=0.
}是等差数列,证明:c=0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中, 椭圆
中, 椭圆![]() 的中心在坐标原点
的中心在坐标原点![]() ,其右焦点为
,其右焦点为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
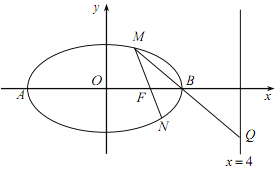
(2)设椭圆的左、右顶点分别为![]() ,
,![]() 是椭圆上异于
是椭圆上异于![]() 的任意一点,直线
的任意一点,直线![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() ,直线
,直线![]() 交直线
交直线![]() 于
于![]() 点, 求证:
点, 求证:![]() 三点在同一条直线上
三点在同一条直线上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 对任意的
对任意的![]() 均有
均有![]() 则称函数
则称函数![]() 具有性质
具有性质![]()
(Ⅰ)判断下面两个函数是否具有性质![]() 并说明理由.
并说明理由.
①![]() ②
②![]()
(Ⅱ)若函数![]() 具有性质
具有性质![]() ,且
,且![]()
求证:对任意![]() 有
有![]()
(Ⅲ)在(Ⅱ)的条件下,是否对任意![]() 均有
均有![]() 若成立,给出证明;若不成立,给出反例.
若成立,给出证明;若不成立,给出反例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com