
 斜率为1的直线l经过抛物线E:y2=2px(p>0)的焦点,且被抛物线所截得弦AB的长为4.
斜率为1的直线l经过抛物线E:y2=2px(p>0)的焦点,且被抛物线所截得弦AB的长为4.分析 (1)求出抛物线的焦点,设出直线l的方程,代入抛物线方程,运用韦达定理和抛物线的定义,可得p=1,进而得到抛物线方程;
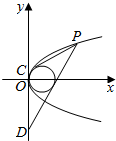
(2)设P(x0,y0),C(0,c),D(0,d)不妨设c>d,直线PC的方程为y-c=$\frac{{y}_{0}-c}{{x}_{0}}$x,由直线和圆相切的条件:d=r,化简整理,结合韦达定理,以及三角形的面积公式,运用基本不等式即可求得最小值.
解答 解:(1)抛物线的焦点为($\frac{p}{2}$,0),直线l的方程:y=x-$\frac{p}{2}$,
与抛物线E:y2=2px联立消去y得(x-$\frac{p}{2}$)2=2px,
∴x2-3px+$\frac{{p}^{2}}{4}$=0,
设A(x1,y1),B(x2,y2),则x1+x2=3p,
又|AB|=|AF|+|BF|=x1+x2+p=4,
所以,3p+p=4,p=1;
(2)设P(x0,y0),C(0,c),D(0,d)不妨设c>d,
直线PC的方程为y-c=$\frac{{y}_{0}-c}{{x}_{0}}$x,
化简得(y0-c)x-x0y+x0c=0,又圆心(1,0)到直线PC的距离为1,
故$\frac{|{y}_{0}-c+{x}_{0}c|}{\sqrt{({y}_{0}-c)^{2}+{{x}_{0}}^{2}}}$=1,即(y0-c)2+x02=(y0-c)2+2x0c(y0-c)+x02c2,
不难发现x0>2,上式又可化为(x0-2)c2+2y0c-x0=0,
同理有(x0-2)d2+2y0d-x0=0,
所以c,d可以看做关于t的一元二次方程(x0-2)t2+2y0t-x0=0的两个实数根,
则c+d=-$\frac{2{y}_{0}}{{x}_{0}-2}$,cd=-$\frac{{x}_{0}}{{x}_{0}-2}$
因为点P(x0,y0)是抛物线Γ上的动点,所以y02=2x0,
所以(c-d)2=(c+d)2-4cd=$\frac{4{{x}_{0}}^{2}}{({x}_{0}-2)^{2}}$,
又x0>2,所以c-d=$\frac{2{x}_{0}}{{x}_{0}-2}$.
所以S△PBC=$\frac{1}{2}$(c-d)x0=x0-2+$\frac{4}{{x}_{0}-2}$+4≥2×2+4=8,
当且仅当x0=4时取等号,此时y0=±2$\sqrt{2}$,
所以△PBC面积的最小值为8,此时P(4,±2$\sqrt{2}$).
点评 本题考查抛物线的定义、方程和性质,主要考查定义法和方程的运用,同时考查直线和抛物线方程联立,运用韦达定理,直线和圆相切的条件:d=r,以及基本不等式的运用,属于中档题.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:解答题
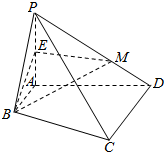 如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AB∥CD,AB⊥AD,CD=2AB,E为PA的中点,M在PD上.
如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AB∥CD,AB⊥AD,CD=2AB,E为PA的中点,M在PD上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 4 | C. | -6 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com